Что такое ОГЭ по математике
Считается, что ОГЭ по математике, который сдают в 9 классе. – простой экзамен по сравнению с ЕГЭ. Так ли это?
26 заданий. Из них 20 задач – с кратким ответом и 6 задач с развернутым ответом, то есть полным и обоснованным решением. На всю эту работу отведено 3 часа 55 минут.
Задания с 1-ого по 20-е оцениваются в 1 балл. Задания 20-26 оцениваются в 2 балла. Максимальный балл, который можно набрать на ОГЭ: 32.
Кстати, а вы знаете, почему продолжительность школьных экзаменов хоть на 5 минут, но меньше, чем 4 часа? Чтобы не кормить. Потому что если длительность экзамена составляет 4 часа или больше, должно быть организовано питание участников экзамена.
Как оцениваются задания ОГЭ по математике?
В 2018 году для получения «тройки» надо было набрать не менее 8 баллов в сумме выполнение заданий обоих модулей, при условии, что из них не менее 2 баллов получено по модулю «Геометрия». Для получения «четверки» не менее 15 баллов и для «пятерки» — от 22 до 32 баллов.
Часто родители девятиклассников считают, что к ОГЭ готовиться не надо и все задания на этом экзамене – на уровне «2+2». Что же там на самом деле?
Действительно, есть и простые задания: вычисления (то есть то, что взрослые всегда считают на калькуляторе), решение квадратных уравнений, задачи на проценты.
Есть задания на анализ графиков и диаграмм (здесь нужна повышенная внимательность), на решение неравенств (а это уже совсем не просто), на свойства и графики функций. Есть 10 заданий по геометрии. Ознакомиться с типовыми вариантами ОГЭ можно здесь: Вариант 1. Вариант 2.
То есть для того чтобы сдать ОГЭ, надо знать на отлично и программу по алгебре, и программу по геометрии. И еще – быть готовым к специфическому формату экзамена: задач много, в условиях множество «подводных камней». Надо быть внимательным и уметь сохранять эту внимательность в течение почти четырех часов.
Задания с выбором ответа в вариантах ОГЭ по математике: помогает или мешает?
В ОГЭ по математике есть и задания с выбором ответа. К сожалению, список возможных ответов — не подсказка, а только дополнительная работа. Например, в задаче №10 надо проанализировать не один график, а целых три. В задаче №14, даже видя перед собой варианты ответов, надо решить неравенство и потом выбрать рисунок, на котором правильно изображены решения этого неравенства. Получается, что «тестовое» задание с выбором ответа сложнее, чем такая же задача без вариантов выбора.
Легко ли сдавать ОГЭ по математике?
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Темы, входящие в ГИА (ОГЭ) по курсу математики
Темы, входящие в ГИА (ОГЭ) по курсу математики — ЕГЭ физмат Skip to content- Числа и вычисления
- Натуральные числа
- Десятичная система счисления. Римская нумерация
- Арифметические действия над натуральными числами
- Степень с натуральным показателем
- Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители
- Признаки делимости на 2, 3, 5, 9, 10
- Наибольший общий делитель и наименьшее общее кратное
- Деление с остатком
- Дроби
- Обыкновенная дробь, основное свойство дроби. Сравнение дробей
- Арифметические действия с обыкновенными дробями
- Нахождение части от целого и целого по его части
- Десятичная дробь, сравнение десятичных дробей
- Арифметические действия с десятичными дробями
- Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной
- Рациональные числа
- Целые числа
- Модуль (абсолютная величина) числа
- Сравнение рациональных чисел
- Арифметические действия с рациональными числами
- Степень с целым показателем
- Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий
- Действительные числа
- Квадратный корень из числа
- Корень третьей степени
- Нахождение приближенного значения корня с помощью калькулятора
- Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби
- Сравнение действительных чисел
- Измерения, приближения, оценки
- Единицы измерения длины, площади, объема, массы, времени, скорости
- Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире
- Представление зависимости между величинами в виде формул
- Проценты. Нахождение процента от величины и величины по ее проценту
- Отношение, выражение отношения в процентах
- Пропорция. Пропорциональная и обратно пропорциональная зависимости
- Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя – степени десяти в записи числа
- Натуральные числа
- Алгебраические выражения
- Буквенные выражения (выражения с переменными)
- Буквенные выражения. Числовое значение буквенного выражения
- Допустимые значения переменных, входящих в алгебраические выражения
- Подстановка выражений вместо переменных
- Равенство буквенных выражений, тождество. Преобразования выражений
- Свойства степени с целым показателем
- Многочлены
- Многочлен. Сложение, вычитание, умножение многочленов
- Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов
- Разложение многочлена на множители
- Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители
- Степень и корень многочлена с одной переменной
- Алгебраическая дробь
- Алгебраическая дробь. Сокращение дробей
- Действия с алгебраическими дробями
- Рациональные выражения и их преобразования
- Свойства квадратных корней и их применение в вычислениях
- Буквенные выражения (выражения с переменными)
- Уравнения и неравенства
- Уравнения
- Уравнение с одной переменной, корень уравнения
- Линейное уравнение
- Квадратное уравнение, формула корней квадратного уравнения
- Решение рациональных уравнений
- Примеры решения уравнений высших степеней. Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители
- Уравнение с двумя переменными; решение уравнения с двумя переменными
- Система уравнений; решение системы
- Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением
- Уравнение с несколькими переменными
- Решение простейших нелинейных систем
- Неравенства
- Числовые неравенства и их свойства
- Неравенство с одной переменной. Решение неравенства
- Линейные неравенства с одной переменной
- Системы линейных неравенств
- Квадратные неравенства
- Текстовые задачи
- Решение текстовых задач арифметическим способом
- Решение текстовых задач алгебраическим способом
- Числовые последовательности
- Понятие последовательности
- Арифметическая и геометрическая прогрессии
- Арифметическая прогрессия. Формула общего члена арифметической прогрессии
- Формула суммы первых нескольких членов арифметической прогрессии
- Геометрическая прогрессия. Формула общего члена геометрической прогрессии
- Формула суммы первых нескольких членов геометрической прогрессии
- Сложные проценты
- Уравнения
- Функции и графики
- Числовые функции
- Понятие функции. Область определения функции. Способы задания функции
- График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства, чтение графиков функций
- Примеры графических зависимостей, отражающих реальные процессы
- Функция, описывающая прямую пропорциональную зависимость, ее график
- Линейная функция, ее график, геометрический смысл коэффициентов
- Функция, описывающая обратно пропорциональную зависимость, ее график. Гипербола
- Квадратичная функция, ее график. Парабола. Координаты вершины параболы, ось симметрии
- График функции
- График функции
- График функции
- Использование графиков функций для решения уравнений и систем
- Числовые функции
- Координаты на прямой и плоскости
- Координатная прямая
- Изображение чисел точками координатной прямой
- Геометрический смысл модуля
- Числовые промежутки: интервал, отрезок, луч
- Декартовы координаты на плоскости
- Декартовы координаты на плоскости; координаты точки
- Координаты середины отрезка
- Формула расстояния между двумя точками плоскости
- Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых
- Уравнение окружности
- Графическая интерпретация уравнений с двумя переменными и их систем
- Графическая интерпретация неравенств с двумя переменными и их систем
- Координатная прямая
- Геометрия
- Геометрические фигуры и их свойства. Измерение геометрических величин
- Начальные понятия геометрии
- Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства
- Прямая. Параллельность и перпендикулярность прямых
- Отрезок. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой
- Понятие о геометрическом месте точек
- Треугольник
- Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений
- Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника
- Прямоугольный треугольник. Теорема Пифагора
- Признаки равенства треугольников
- Неравенство треугольника
- Сумма углов треугольника. Внешние углы треугольника
- Зависимость между величинами сторон и углов треугольника
- Теорема Фалеса
- Подобие треугольников, коэффициент подобия. Признаки подобия треугольников
- Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от до
- Решение прямоугольных треугольников. Основное тригонометрическое тождество. Теорема косинусов и теорема синусов
- Многоугольники
- Параллелограмм, его свойства и признаки
- Прямоугольник, квадрат, ромб, их свойства и признаки
- Трапеция, средняя линия трапеции; равнобедренная трапеция
- Сумма углов выпуклого многоугольника
- Правильные многоугольники
- Окружность и круг
- Центральный, вписанный угол; величина вписанного угла
- Взаимное расположение прямой и окружности
- Касательная и секущая к окружности; равенство отрезков касательных, проведенных из одной точки
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Вписанные и описанные окружности правильного многоугольника
- Измерение геометрических величин
- Длина отрезка, длина ломаной, периметр многоугольника. Расстояние от точки до прямой
- Длина окружности
- Градусная мера угла, соответствие между величиной угла и длиной дуги окружности
- Площадь прямоугольника
- Площадь параллелограмма
- Площадь трапеции
- Площадь треугольника
- Площадь круга, площадь сектора
- Формулы объема прямоугольного параллелепипеда, куба, шара
- Векторы на плоскости
- Вектор, длина (модуль) вектора
- Равенство векторов
- Операции над векторами (сумма векторов, умножение вектора на число)
- Угол между векторами
- Коллинеарные векторы, разложение вектора по двум неколлинеарным векторам
- Координаты вектора
- Скалярное произведение векторов
- Геометрические фигуры и их свойства. Измерение геометрических величин
- Статистика и теория вероятностей
- Описательная статистика
- Представление данных в виде таблиц, диаграмм, графиков
- Средние результатов измерений
- Вероятность
- Частота события, вероятность
- Равновозможные события и подсчет их вероятности
- Представление о геометрической вероятности
- Комбинаторика
- Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения
- Описательная статистика
egefizmat.ru
Разбор и решение задания №14 ОГЭ по математике
Уравнения, неравенства и их системы
В задании №14 проверяется умение решать уравнения, неравенства и их системы. Конечно, под такие слова подходит огромный спектр заданий. Уточнение, пожалуй, одно. Надо применять графическое представление решения и показа результатов этого решения. В демонстрационном варианте ОГЭ предложена система двух линейных неравенств и графические представления вариантов ответов. Полезно понимать, что главным здесь является решение конкретных неравенств и понимание геометрического смысла полученного решения.
Ответом в задании 14 является одна из цифр 1; 2; 3; 4, соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №14
Определение:
Неравенством называется выражение вида:
a < b (a ≤ b), a > b (a ≥ b)
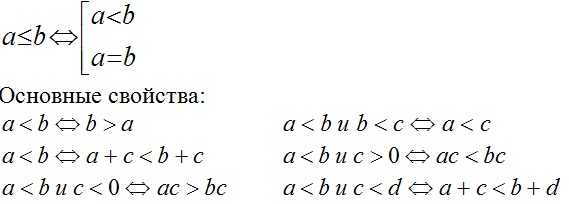
Полезным для нас окажется метод интервалов:
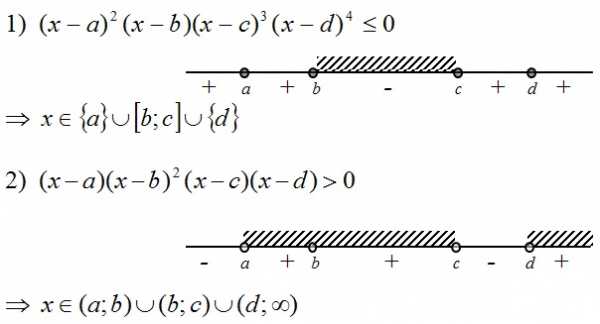
Разбор вариантов задания №14 ОГЭ по математике
Первый вариант задания
Укажите решение неравенства: 2 x — 3 ( x — 7) ≤ 3
Решение:
Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число — в этих случаях знак неравенства будет меняться на противоположный!
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает + 21:
2 x — 3 x + 21 ≤ 3
Затем приводим подобные, перенося числа в правую сторону:
2 x — 3 x ≤ 3 — 21
— x ≤ -18
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
x ≥ 18
Таким образом, мы получаем, что x должен быть больше либо равен 18.
Ответ: [18; +∞)
Второй вариант задания
В данном случае мы имеем дело с квадратным неравенством:
Укажите множество решений неравенства:
7 x — x2 < 0
Решение:
Существуют несколько способов решения квадратных неравенств, но я приведу самый простой и надежный. В начале выносим x за скобку, так как это неполное квадратное неравенство:
x ( 7 — x ) < 0
Затем находим ноли функции x ( 7 — x ) = 0, приравнивая каждый множитель к нолю:
x = 0
7 — x = 0
Получаем:
x = 0
x = 7
Таким образом, мы получили три интервала:
( -∞ ; 0 )
( 0 ; 7 )
( 7 ; +∞)
Подставим любое значение x из первого интервала и посмотрим на получившийся ответ.
Подставим -1:
x ( 7 — x ) = — 1 ( 7 — (-1) ) = -8
Значение отрицательно, значит в интервале ( -∞ ; 0 ) функция отрицательна, что нам и подходит для ответа, так как в условии:
x ( 7 — x ) < 0
Подставим 1:
x ( 7 — x ) = 1 ( 7 — 1 ) = 6
Значение положительно, и промежуток ( 0 ; 7 ) нам не подходит.
Подставим 8:
x ( 7 — x ) = 8 ( 7 — 8 ) = — 8
Значение отрицательно, и это подходит под условия, следовательно ответ:
( -∞ ; 0 ) и ( 7 ; +∞)
или графически:
Третий вариант задания
Укажите множество системы неравенств:
⌈ x — 4 ≥ 0
⌊ x — 0,3 ≥ 1
Решение:
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
⌈ x ≥ 4
⌊ x ≥ 1,3
В отличие от первого примера, решение более простое, но в данном случае нужно сравнить промежутки и выбрать общий. Первое неравенство требует, чтобы x был больше 4, а второе — более 1,3, на координатной прямой это будет выглядеть следующим образом:
Промежутки перекрывают друг друга начина с 4, значит ответ выглядит следующим образом (не забываем, что неравенство нестрогое):
[ 4 ; + ∞ ) или
Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)
Решите систему неравенств:
На каком рисунке изображено множество её решений?
Решение:
Итак, решим систему неравенств — оставим х в левой части, а остальное перенесём в правую, получим:
х ≤ 0 -2,6
х ≥ 1 — 5
Вычислив, получаем ответ:
х ≤ -2,6
х ≥ -4
Найдем его на координатной прямой — это №2.
Ответ: 2
spadilo.ru
Пробник по ОГЭ — Жизнь в пригороде

(на фото демо вариант заданий на ОГЭ по математике)
Добрый вечер! Как я говорил ранее, на следующей неделе во вторник 17 марта, я пишу пробный экзамен ОГЭ(Общая государственная атистация) по математике, в прошло году его еще называли ГИА(Государственная итоговая атестация). Он будет проходить в школе №20 пос.Сокол, так как если сдающих экзамен менее 15 человек, они едут в ближайшую школу, в которой есть 15 человек сдающих этот зкзамен. Экзамен начнется в 10 часов по местному времени и будет идти в течении 235 минут, то есть 3 часа 55 минут. Подробнее под катом…
2.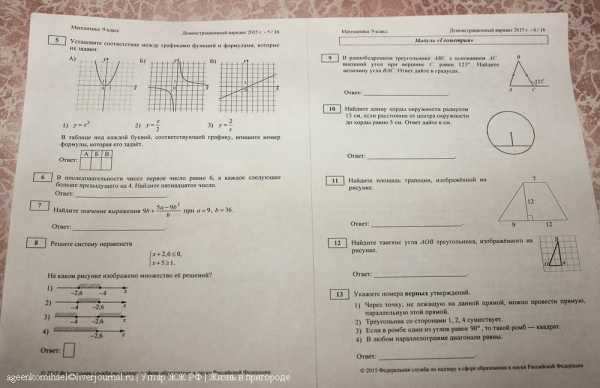
Задания состоят из трех модулей Алгебра 8 заданий, Геометрия 5 заданий и Реальная математика 7 заданий, а также есть еще вторая часть, в которой задания повышенной сложности 3 по Алгебре и 3 по Геометрии.
3.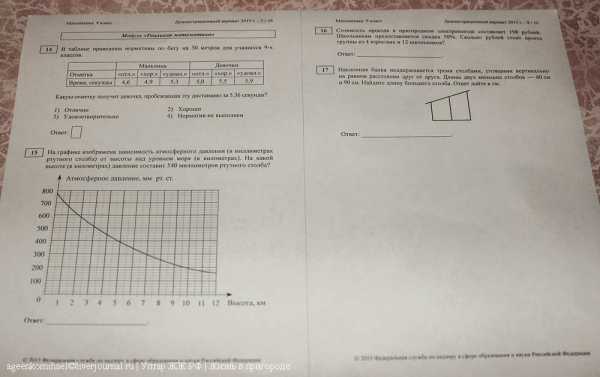
Для тех кто хочет получить три надо решить от 8 до 16 заданий, причем надо решить не менее 3 заданий по алгебре, двух по геометрии и двух по реальной математике, если сделать например два по алгебре, но три по геометрии или реал математике, то экзамены не защитают. Оценка 4 начинается с 16 заданий или 16 баллов(в первой части все задания оцениваются в один бал, а во второй оценивание идет по возрастающей 2, 3 и 4 балла соответственно). Оценку 5 можно получить если ты наберешь вроде бы как не менее 23-х баллов.
4.
5.
(на фото мой бланк, я делал вариант из этого поста и ответы первой части можно сверить с ответами в бланке)
Вот так выглядит бланк ответов, для заданий второй части выдается отдельный бланк, который проверяют люди, а бланк ответов №1 проверяет компьютер. В том что проверяет компьютер есть свой геморой, там надо писать каждую цифру, запятую, букву и т.п. в каждую клеточку, причем они должны быть еще написаны правильным образом как указано в рамке с буквами и цифрами. В общем будет не легко, хотя это еще зависти от того, какой вариант попадется, легкий или трудный, как фортанет…)
Если понравилось или есть, что сказать пишите коменты, ставьте лайки и делитесь с друзьями…
ageenkomihael.livejournal.com
Разбор и решение задания №4 ОГЭ по математике
Числа, вычисления и алгебраические выражения
Четвертое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.
При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.
В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.
Ответом в задании 4 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №4
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.
Разбор типовых вариантов задания №4 ОГЭ по математике
Первый вариант задания
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Решение:
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2
Второй вариант задания
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Решение:
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый
Ответ: 1
Третий вариант задания
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Решение:
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: 3
Четвертый вариант задания
По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:
Какое из данных ниже чисел является значением выражения?
Решение:
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
16 — 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4
Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!
Пятый вариант задания (демонстрационный вариант ОГЭ 2017)
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
Решение:
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3
spadilo.ru
Разбор и решение задания №11 ОГЭ по математике
Арифметические и геометрические прогрессии
В одиннадцатом задании мы сталкиваемся с прогрессиями — общими понятиями.
Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые.Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.
Ответом в задании 11 является целое число или конечная десятичная дробь.
Теория к заданию №11
Начнем теоретическую справку об определениях прогрессий.
Арифметическая прогрессия:
Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.
an+1 = an + d
где d – разность прогрессии
Геометрическая прогрессия:
Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.
bn+1 = bn q
где q – знаменатель прогрессии
В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.
Разбор типовых вариантов задания №11 ОГЭ по математике.
Первый вариант задания (нахождение разности прогрессии)
Дана арифметическая прогрессия a(n) в которой
a (3) = 6,9
a (16) = 26,4
Найдите разность прогрессии.
Решение:
Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).
Находим разницу между значениями a (3) и a (16):
a (3) — a (16) = 26,4 — 6,9 = 19,5
Находим количество членов:
16 — 3 = 13
Находим разность прогрессии:
19,5 / 13 = 1,5
Ответ: 1,5
Второй вариант задания (нахождение неизвестного члена)
Выписано несколько последовательных членов геометрической прогрессии:
-1, x, -49, -343, ….
Найдите x.
Решение:
Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:
-343 / -49 = 7
Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.
x = -49 / 7 = -7
Ответ: -7
Третий вариант задания (нахождение n-ого члена)
Выписаны первые несколько членов арифметической прогрессии: 10, 6, 2, …
Найдите 101 член.
Решение:
Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:
an = a1 + (n-1) • d
В нашем случае:
a1 = 10
d = 6 — 10 = -4
Подставляем значения в формулу:
a101 = 10 + (101-1) • (-4) = -390
Ответ: -390
Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)
В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.
Решение:
В данном задании нас проверяют на знание формулы арифметической прогрессии:
где n — номер члена прогрессии, d — разность, а а1 — первый член.
Решение:
Подставим в общую формулу известные из условия значения:
d = 4,
а1 = 6,
n = 15,
получим:
a15 = 6 + (15 — 1) • 4
вычислив, получаем значение 15 члена:
a15 = 62
Ответ: 62
spadilo.ru
Разбалловка ОГЭ — это что такое?
Основной государственный экзамен (ОГЭ) является обязательным для всех школьников, заканчивающих 9 класс. Экзамен — это не только объективная проверка знаний, но и большой стресс для школьников. Для того чтобы избежать паники на тесте, нужно заранее узнать критерии разбалловки ОГЭ. О них вы сможете прочесть в этой статье.
ОГЭ – цели и задачи
Обязательный государственный экзамен является аналогом ЕГЭ в 11 классе. Можно считать его подготовкой к более серьезному испытанию – поступлению в вуз. Для 9-классников ОГЭ тоже кажется огромной проблемой. Дело в том, что сдавать этот тест должны все школьники, заканчивающие 9 класс, независимо от того, покидают ли они среднее учебное заведение или остаются в нем дальше.

ОГЭ является также одной из составляющих ГИА. Учащийся может выбрать – остановиться только на обязательных предметах или испытать свои знания в дополнительных дисциплинах. Как бы то ни было, список предметов в ОГЭ давно распределен:
- русский язык;
- математика.
Еще две дисциплины школьник может выбрать себе сам. Ходят слухи, что Министерство образования собирается ввести еще один обязательный экзамен – пятый по счету. Каждый год правила проведения государственных экзаменов ужесточаются. Коснулось это и тестов в 2017 году: оценки за обязательные предметы стали суммироваться с результатами экзамена, была внедрена аттестация в четвертом классе. Улучшит ли эта система реальные знания школьников, покажет время. А пока нужно обратиться к интерпретации полученных баллов за основной государственный экзамен.
Что такое разбалловка?
Разбалловка ОГЭ – это перевод результатов экзамена в балльную систему. Получая за каждое задание определенное количество баллов, школьник в уме может прикинуть, какой его предварительный результат. Таблицу перевода обновляют каждый год, поэтому ученикам, сдающим ОГЭ, ни в коем случае нельзя ориентироваться на показатели предыдущих лет. Что же касается оценок за экзамены, то их официально отменили еще в 2008 году.
Но школьники и преподаватели все еще по привычке переводят результаты за тесты в пятибалльную систему. В большинстве предметов «пятерки» начинаются от 33 баллов. Правда, на результаты поступления эти переводы все равно не повлияют: при приеме в среднее учебное заведение учитывается итоговая сумма, которая складывается из всех результатов.
Разбалловка ОГЭ
Какой документ определяет количество баллов, получаемых за каждое задание ОГЭ? Эту информацию берут из распоряжения Рособрнадзора, которое Министерство образования выпускает каждый год. Зеленая область в таблице разбалловки означает отличную подготовленность ученика к экзамену. Если итоговое количество баллов за предмет отмечено зеленым, это означает, что ученик комплексно и системно изучил предмет и в полной мере понимает его.
Желтая область указывает на среднюю подготовку. Как правило, это удовлетворительный результат для большинства школьников, сдающих ОГЭ. И, наконец, красная зона говорит о том, что учащийся не сдал экзамен и его знания по предмету неудовлетворительны.

Узнать, сколько баллов дает каждое задание, можно в демоверсиях экзаменов, которые доступны в электронном варианте. В них ученик сможет не только проверить качество выполнения заданий, но и потренироваться в решении задач.
Разбалловка в 2018 году

Разбалловка ОГЭ-2018 пугает многих школьников и их родителей. Многие начинают готовиться к этому экзамену за год, а то и за два. Ведь всем хочется получить максимально возможные оценки за тест. Какие изменения принесет 2018 год школьникам:
- Увеличение количества экзаменов: многие родители хотят вообще отменить обязательный государственный экзамен, но пока что его правила только ужесточаются. С 2016 года для учащихся стали обязательными не два, а уже четыре экзамена. Эксперты ФИПИ объясняют это нововведение тем, что так школьники будут больше «подкованы» в разных областях знаний, а не только в математике и русском языке.
- В 2018 году планируется внедрение пятого обязательного предмета. Данное новшество призвано существенно повлиять на успеваемость и успешность учеников.
- Оценка, которую ученик получит за обязательный экзамен, будет обязательно учтена в аттестате.
- Документы об окончании среднего учебного заведения будут выдаваться только тем, кто сдал хотя бы четыре из пяти предметов. Эта мера призвана повысить мотивацию и, как следствие, уровень успеваемости учеников. Эффективна ли она будет – покажет время.
Разбалловка по математике
Математика – один из самых важных обязательных предметов в 9 классе, и один из самых непростых. Набрать максимальное количество баллов по этой дисциплине могут только самые умные и образованные ученики. Разбалловка ОГЭ 2018 в математике дает возможность получить максимальное количество баллов – 32.
За модуль с алгебраическими заданиями школьник может набрать 12 баллов, за геометрические тесты – 11 баллов и за модуль «Реальная математика» — 7 баллов. Последняя часть работы содержит наиболее нестандартные и интересные задания, решить которые будет непросто.
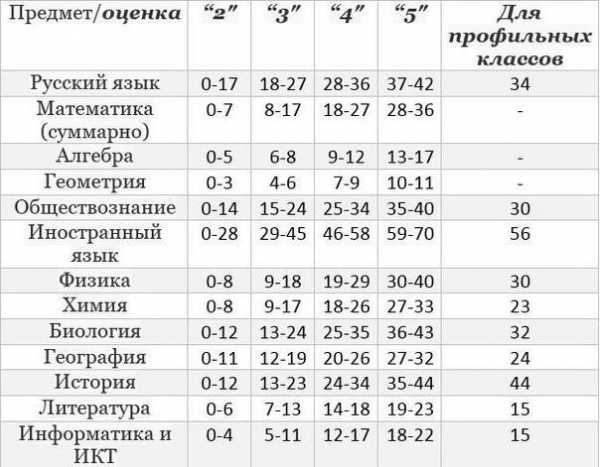
Минимальный результат работы, который даст возможность считать экзамен сданным, составляет 8 баллов. Набрать это количество не составит особого труда, особенно, если вы тщательно готовились к тесту. Разбалловка ОГЭ по математике позволяет заранее узнать свой результат задолго до официального объявления оценок. Любой результат, который выше 22 баллов, будет засчитан как «отлично» за предмет. Набрав такое количество, вы уже можете не волноваться о том, что будет в аттестате – однозначно, только хорошая оценка.
Разбалловка по русскому
Экзамен по самому «великому и могучему» языку предполагает за все решенные задания максимум 39 баллов. Разбалловка ОГЭ по русскому выглядит следующим образом:
- 34-39 балла – гарантирует отличную оценку.
- 25-30 баллов претендуют на твердую «четверку».
Но есть в разбалловке ОГЭ по русскому и некоторые нюансы. Для получения отметки «4», ученик должен получить не менее четырех баллов за грамотность. Если баллов набирается меньше, то выставляется отметка «3». Для отличной оценки школьник должен набрать за грамотность не менее шести баллов.
Перевод баллов по обществознанию

Разбалловка ОГЭ в обществознании осуществляется примерно так же, как и в предыдущих предметах:
- Максимальное количество баллов также составляет 39. «Пятерки» начинаются от 34 баллов и выше.
- Для «четверки» нужно будет набрать от 25 до 33 баллов.
- «Тройку» получат те, кто получил результат 15-24 балла.
- Несданным экзамен считается, если школьник набрал менее 25 баллов. Если же ученик собирается поступать в среднее специальное учреждение, то минимальная оценка составит 30 баллов.
По сравнению с математикой, разбалловка ОГЭ по обществознанию 2018 проводится гораздо строже. И тому есть объяснения, этот предмет редко выбирают те, кто собирается просто перейти в 10 класс. А для профильных учреждений уровень знаний должен быть достаточно высоким.
Разбалловка ОГЭ по биологии
В экзамене «Биология» школьник может набрать максимум 46 баллов. Из них 37 понадобятся для «пятерки», а если вы не стремитесь к отличным результатам, то вам достаточно будет и 26-36 баллов, которые дадут оценку «4». Если вы наберете меньше 25 баллов, это будет считаться «тройкой». Ну, а для того чтобы совсем не сдать дисциплину, нужно набрать меньше 13 баллов (или меньше минимума в 33 балла для обучения в профильном классе).
Разбалловка по химии
Разбалловка ОГЭ по химии показывает, что максимальное возможное количество баллов – 34.
- «Пятерка» начинается от 27 баллов.
- «Четверка» – от 18 до 26.
- «Тройка» — от 9 до 17.
- Экзамен считается несданным, если ученик набрал меньше 9 баллов.
Апелляция ОГЭ
Если учащийся не согласен с выставленными результатами или недоволен проведением экзамена, то он всегда может подать апелляцию. Удовлетворят его запрос или нет будет зависеть от того, насколько справедливы его требования. Бывают такие ситуации, во время которых школьник отвлекается на происходящее вокруг и в результате неправильно решает полученные задания.
Такие моменты могут послужить причиной для подачи подобного заявления. Важно подать его в течение двух дней после сдачи экзамена, иначе аппеляцию просто не примут. По результатам рассмотрения заявления количество баллов может быть пересчитано, причем, как в большую, так и в меньшую сторону. Сама экзаменационная работа будет перепроверена полностью.

Советы преподавателей
Преподаватели, повидавшие на своем опыте немало учеников, сдающих государственные экзамены, в голос говорят о том, что главное при подготовке к ОГЭ – это психологический комфорт ученика. Естественно, что экзамен является сильным стрессом, в результате которого многие ученики в прямом смысле теряют способность мыслить здраво. Тем не менее, собранность и здравый смысл окажут первостепенное значение при решении задач. Поэтому специалисты рекомендуют практиковать йогу, дыхательные практики, но при этом отказаться от приема лекарственных препаратов, угнетающих нервную систему.
Второй важный пункт подготовки — это, собственно, сама подготовка к экзамену. Занятия с репетиторами, посещение дополнительных курсов за год до ОГЭ помогут даже самому «пропащему» ребенку сдать экзамены на минимальные оценки.

Итоги
Обязательные государственные экзамены являются тяжелым испытанием для школьников и их родителей. Немного упростить ситуацию может разбалловка ОГЭ, которая позволяет наглядно понять, какую оценку получил ребенок. Пусть она и не вписывается в аттестат, но все же косвенно на него влияет и служит важным доказательством знаний ученика.
Ориентируясь на таблицу перевода баллов по пятибалльной системе, школьник сможет заранее узнать, какое значение необходим для получения «пятерки», «тройки» или «четверки», и ориентироваться на него. Кроме того, разбалловка ОГЭ может помочь и после сдачи экзамена: придя домой, ученик может сразу посчитать примерное количество баллов, которое он получил за экзамен, что избавит от долгого и томительного ожидания результатов.
fb.ru
