Перевод чисел из одной системы счисления в другую онлайн
Результат уже получен!
Системы счисления
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
| число | 6 | 3 | 7 | 2 |
| позиция | 3 | 2 | 1 | 0 |
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·103+3·102+7·101+2·100
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
| число | 1 | 2 | 8 | 7 | . | 9 | 2 | 3 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10
В общем случае формулу можно представить в следующем виде:
Цn·sn+Цn-1·sn-1+…+Ц1·s1+Ц0·s0+Д-1·s-1+Д-2·s-2+…+Д-k·s-k
(1)
где Цn-целое число в позиции n, Д-k— дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1·26+0·25+1·24+1·23+1·22 +0·21+1·20+0·2-1+0·2-2+1·2-3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C— на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4. Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 2 | 2 | |||||
| 0 | 2 | 1 | |||||
| 0 |
Рис. 1
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111. Следовательно можно записать:
15910=100111112.
Пример 5. Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
Рис. 2
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147(см. Рис. 2). Следовательно можно записать:
61510=11478.
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Рис. 3
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Далее рассмотрим перевод правильных десятичных дробей в двоичную СС, в восьмеричную СС, в шестнадцатеричную СС и т.д.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Рис. 4
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011.
Следовательно можно записать:
0.21410=0.00110112.
Пример 8. Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Рис. 5
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
0.12510=0.0012.
Пример 9. Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Рис. 6
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0.21410=0.36C8B416.
Пример 10. Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Рис. 7
Получили:
0.51210=0.4061118.
Пример 11. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
159.12510=10011111.0012.
Пример 12. Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим:
19673.21410=4CD9.36C8B416.
matworld.ru
Правила перевода чисел из одной системы счисления в другую
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒
Из 16 или 8 в 2
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр) (см. таблицу). | |||||||
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||||
| триады | тетрады | ||||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
Например:
а) Перевести 305.48 «2» с.с.
б) Перевести 7B2.E16«2» с.с.
16А16=1 0110 10102 3458=11 100 1012
Из 2 в 16 или 8
| Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например:
а) Перевести 1101111001.11012 «8» с.с.
б) Перевести 11111111011.1001112 «16» с.с.
10001010100101012=1000 1010 1001 0101=8A9516= 1 000 101 010 010 101=1052258
Из 16 в 8 и обратно
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Например:
Перевести 175.248 «16» с.с.
Результат: 175.248 = 7D.516.
Из 10 в любую с.с.
| При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. |
Например:
а) Перевести 18110 «8» с.с.
Результат: 18110 = 2658
б) Перевести 62210 «16» с.с.
Результат: 62210 = 26E16
Перевод правильных дробей
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Например:
Перевести 0.312510 «8» с.с.
Результат: 0.312510 = 0.248
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Например:
Перевести 0.6510 «2» с.с. Точность 6 знаков.
Результат: 0.6510 0.10(1001)2
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Например:
Перевести 23.12510 «2» с.с.
| 1) Переведем целую часть: | 2) Переведем дробную часть: |
Таким образом: 2310 = 101112; 0.12510 = 0.0012.
Результат: 23.12510 = 10111.0012.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Из 2, 8 или 16 в 10
| При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. |
Например:
a)10101101.1012 = 1 27+ 0 26+ 1 25+ 0 24+ 1 23+ 1 22+ 0 21+ 1 20+ 1 2-1+ 0 2-2+ 1 2-3 = 173.62510
б) Перевести 703.048 «10» с.с.
703.048 = 7 82+ 0 81+ 3 80+ 0 8-1+ 4 8-2 = 451.062510
в) Перевести B2E.416 «10» с.с.
B2E.416 = 11 162+ 2 161+ 14 160+ 4 16-1 = 2862.2510
Схема перевода чисел из одной системы счисления в другую

Aрифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0 0=0 0 1=0 1 0=0 1 1=1 |
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Например:
Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;
Результат 1101+101+111=11001.
Таблица сложения в 8-ой системе счисления
| 2+2=4 | 3+2=5 | 4+2=6 | 5+2=7 | 6+2=10 | 7+2=11 |
| 2+3=5 | 3+3=6 | 4+3=7 | 5+3=10 | 6+3=11 | 7+3=12 |
| 2+4=6 | 3+4=7 | 4+4=10 | 5+4=11 | 6+4=12 | 7+4=13 |
| 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | 6+5=13 | 7+5=14 |
| 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | 7+6=15 |
| 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
Таблица сложения в 16-ой системе счисления
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
Вычитание
Рекомендуемые страницы:
lektsia.com
Системы счисления. Правила перевода из 2-й в 8-ую и 16-ричную СС и наоборот

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления и наоборот

Перевод чисел внутри родственных систем (в частности, с основанием 2, 8 и 16) упрощен, поскольку все цифры алфавита для систем с большим основанием можно представить совокупностью цифр системы с наименьшим основанием:
№
1
Основание системы счисления
Числа
2
10
3
Десятеричная
2
0
1
0000
4
Двоичная
8
16
0001
2
Восьмеричная
0
0
1
Шестнадцатеричная
0010
3
1
2
0011
4
2
5
3
0100
0101
6
4
3
4
7
5
0110
0111
8
5
6
6
7
1000
9
7
10
1001
10
11
8
11
1010
12
1011
12
9
A
1100
13
13
B
14
1101
14
15
C
15
1110
1111
D
16
E
17
F

Перевод целых чисел.
- Правило Чтобы перевести целое двоичное число в восьмеричную (8=2 3 ) систему счисления необходимо:
- • разбить данное число справа налево на группы по 3 цифры в каждой;
- • рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления.



Задание:
- Перевести из 2 → 8
- 10110110
- 100011001
- 1110111

Задание:
- Перевести из 2 → 8
- 10110110 2 =266
- 100011001 2 =431 8
- 1110111 2 =167 8

- Правило Чтобы перевести целое двоичное число в 16-ричную (16=2 4 ) систему счисления необходимо:
- • разбить данное число справа налево на группы по 4 цифры в каждой;
- • рассмотреть каждую группу и записать ее соответствующей цифрой 16-ричной системы счисления.



Задание:
- Перевести из 2 → 16
- 10110110
- 100011001
- 1110111

Задание:
- Перевести из 2 → 8 → 16
- 10110110 2 = 266 8 =В6 16
- 100011001 2 =431 8 = 119 16
- 1110111 2 =167 8 =77 16

Перевод дробных чисел
- П равило Чтобы перевести дробное двоичное число в восьмеричную (шестнадцатеричную) систему счисления необходимо:
- • разбить данное число, начиная от запятой влево целую часть и вправо дробную часть на группы по 3 (4) цифры в каждой;
- • рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной (шестнадцатеричной) системы счисления.




Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления.
- Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления.


Найдите где нужно поставить запятую

Перевести в 2-ю систему счисления
- 427 8 =
- 216 8 =
- 1072 8 =
- 427 16 =
- А41 16 =
- 1С4В 16 =

Перевести в 2-ю систему счисления
- 427 8 =100010111 2
- 216 8 =10001110 2
- 1072 8 =1000111010 2
- 427 16 =10000100111 2
- А41 16 =101001000001 2
- 1С4В 16 =110001001011 2

Проверочная работа Перевести числа в соответствующие СС. 1 вариант 2 вариант
2
2
8
8
101110
16
16
152
251
4В5
101100
2А4
videouroki.net
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Системы счисления — Перевод чисел из одной системы счисления в другую
Перевод чисел в десятичную систему счисления
Перевод из двоичной системы в десятичную
Преобразуем двоичное число 1001011 из первого примера
Пример Перевести число 11010101 из двоичной системы в десятичную.
Преобразуем число:110101012= 1 * 27 + 1 * 26 + 0 * 25 + 1 * 24 + 0 * 23 + 1 * 22 + 0 * 21 + 1 * 20=128+64+0+16+0+4+0+1=21310
Перевод из восьмеричной системы в десятичную
Преобразуем восьмеричное число 572.
Пример Перевести число 572 из восьмеричной системы в десятичную.
Преобразуем число:5728=5 * 82 + 7 * 81 + 2 * 80=320+56+2=37810
Перевод из шестнадцатеричной системы в десятичную
Числа в шестнадцатеричной системе состоят из цифр 0-9 и букв A, B, C, D, E, F, таблица соответствия:
| десятичная | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| шестнадцатеричная | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Преобразуем шестнадцатеричное число A5C.
Пример Перевести число A5C из шестнадцатеричной системы в десятичную.
Преобразуем число:A5C16= 10 * 162 + 5 * 161 + 12 * 160 =2560+80+12=265210
calcs.su
Системы счисления
СИСТЕМЫ СЧИСЛЕНИЯ
СПОСОБЫ ПЕРЕВОДА ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ
I. Перевод целых чисел из десятичной системы счисления в q-ичную.
II. Перевод чисел из q-ичной системы счисления в десятичную.
III. Перевод чисел из 2-ичной системы счисления в 2n-ичную.
IV. Перевод чисел из 2n-ичной системы счисления в двоичную.
I. ПЕРЕВОД ЧИСЕЛ (ЦЕЛЫХ И ДРОБНЫХ) ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В Q-ИЧНУЮ
1) разделить целое число на основание новой системы счисления q, записать частное от деления и остаток;
2) затем полученное частное снова разделить на q и записать частное и остаток; и так делить до тех пор, пока в частном не получится ноль;
3) составить число в новой системе счисления, записав полученные остатки в обратном порядке.
Перевод чисел из 10-й системы счисления в 2-ую
Пример 1.
1 способ
 4610→1011102
4610→1011102
2 способ
Десятичное число/ целое частное | Делитель (основание число) | Остаток | Цифры двоичного числа |
46 | 2 | 0 | a0 |
23 | 2 | 1 | a1 |
11 | 2 | 1 | a2 |
5 | 2 | 1 | a3 |
2 | 2 | 0 | a4 |
1 | 2 | 1 | a5 |
Перевод чисел из 10-й системы счисления в 8-ую
Пример 2.
1 способ
4610→568
2 способ
Перевод чисел из 10-й системы счисления в 16-ую
Пример 3.
1 способ
4610→2E16
2 способ
II. ПЕРЕВОД ЧИСЕЛ ИЗ Q-ИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
пронумеровать каждую цифру q-ичного числа следующим образом: целую часть нумеруем, начиная с 0, справа налево в сторону увеличения, а дробную часть, начиная с –1, слева направо в сторону уменьшения;
каждую цифру q-ичного числа умножить на основание системы счисленияqв соответствующей степени;
выполнить арифметические действия.
Перевести число 1011102 в 10-ю систему счисления
Пример 4.
1011102→4610
Перевести число 568 в 10-ю систему счисления
Пример 5.
568→4610
Перевести число 2E16 в 10-ю систему счисления
Пример 6.
2E16→ 4610
III. ПЕРЕВОД ЧИСЕЛ ИЗ 2-Й СИСТЕМЫ СЧИСЛЕНИЯ В 2N-ИЧНУЮ
Разбить исходное число на группы по nцифр в каждой (целая часть – налево, дробная часть – направо), дописав слева и справа нужное количество нулей.
Перевести каждую группу в систему счисления с основанием 2n(см. табл. 1).
Перевести число 1011102 в 8-ую систему счисления
Пример 7.
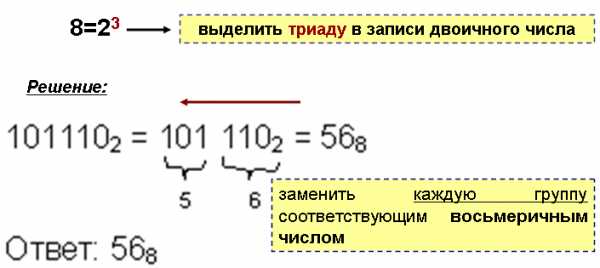
1011102→568
Перевести число 1011102 в 16-ую систему счисления
Пример 8.

1011102→2E16
IV. ПЕРЕВОД ЧИСЕЛ ИЗ 2N-ИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДВОИЧНУЮ
Обратный переход из системы счисления с основанием 2nосуществляется заменой каждой цифры исходного числа соответствующимn-разрядным двоичным числом. Для перевода в 8-ичную и 16-ичную систему счисления используйте таблицу, рассмотренную ранее (см. табл. 1).
Перевод чисел из 8-й системы счисления в 16-ую
Перевести число 568 в 2-ую систему счисления
Пример 9.
568→1011102
Перевести число 2E16 в 2-ую систему счисления
Пример 10.
2E16→1011102
Перевод чисел из 8-й системы счисления в 16-ую
Перевести число 568 в 16-ую систему счисления
Пример 11.
568→2E16
Таблица 1
Двоичная, восьмеричная и шестнадцатеричная системы счисления
8-ичная система | 2-ичная система | 16-ичная система | 2-ичная система |
0 | 000 | 0 | 0000 |
1 | 001 | 1 | 0001 |
2 | 010 | 2 | 0010 |
3 | 011 | 3 | 0011 |
4 | 100 | 4 | 0100 |
5 | 101 | 5 | 0101 |
6 | 110 | 6 | 0110 |
7 | 111 | 7 | 0111 |
8 | 1000 | ||
9 | 1001 | ||
A (10) | 1010 | ||
B (11) | 1011 | ||
C (12) | 1100 | ||
D (13) | 1101 | ||
E (14) | 1110 | ||
F (15) | 1111 |
5
studfiles.net
Как перевести число из одной системы в другую
Как перевести число из одной системы счисления в другую ?
Перевод из Х позиционной системы в 10-ную
Прежде всего мы рассмотрим перевод
целого числа из любой системы счисления в
10-ную. Надо напомнить что в позиционной
системе счисления число можно записать с
помощью формулы:
N = an-1qn-1 + an-2qn-2 +…+ a1p1
+ a0p0
Где N — любое
произвольное число;
q — основание системы;
an-1
— значение разряда в числе;
n — кол-во разрядов в числе;
Для того
чтобы перевести число из любой системы
счисления в 10-ную надо:
1. Записать это число по формуле записи
числа в в позиционной системе.
2. В качестве основания взять взять
основание той системы из которой
производиться перевод.
3. Произвести вычисления в 10- ой системе
счисления.
123(8) = 1*82+2*81+3*80 = 64
+16 +3 = 83(10)
123(5)
= 1*52+2*51+3*50 = 25+10 +3 = 38(10)
Можно
заметить что чем больше основание
системы тем длиннее запись числа.
Перевод дробной части из 10-ой в 2-ую
1. Последовательно выполнять
умножение исходной десятичной дроби и
получаемых дробных частей произведений
на основание системы (2), до тех пор пока не
получиться нулевая дробная часть или не
будет достигнута требуемая точность вычислений.
2. Записать полученные целые части
произведения в прямой
последовательности.
1) 0,125(10) =>
0,001(2)
2) 0,28(10)=>0,010001(2)
0|125
0|28
0|250
0|56
0|500
1|12
1|000
0|24
0|48
0|96
1|92
Перевод из 10-ой системы счисления в 2-ую, 8-ую, 16-ую.
Чтобы перевести число из десятичной
системы в двоичную(8-ую, 16 -ую) надо
производить последовательное деление на
2 (8, 16) до тех пор пока в частном не
получиться число меньше делителя.
В качестве
результата записать последние значения
частного и выписать за ним все остатки в
обратном порядке.
1. Способ: 1) 40(10)= >
101000(2)
2)
123(10)=>173(8)
3) 123(10)=>7B
2. Способ: 71(10)=> 100111(2)
71|1
35|1
17|1
8 |0
4 |0
2 |0
1
Перевод чисел из 2-ой в 8-ую(16-ую) и обратно.
Чтобы перевести число из 8-ой(16-ой) системы
в 2-ую надо каждый разряд восьмеричного (16-ого)
числа записать триадами(четвёрками), т.е
двоичными разрядами согласно таблице.
| 10-ая | 2-ая | 8-ая | 16-ая |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 |
0 1 2 3 4 5 6 7 8 9 A B C D E F |
Чтобы перевести число из двоичной системы в 8-ую(16-ую) надо начиная с младшего разряда разбить число на триады(четверки), а потом каждую из триад(четверок) заменить соответствующей цифрой в 8-ой(16-ой) системе.
syssch.narod.ru
