Школьникам отменили ЕГЭ по базовой математике
В этом году выпускники будут сдавать те предметы, которые необходимы для поступления в вуз.
Обязательных предметов раньше было два: русский и математика. При этом с 2019 года участники ЕГЭ вправе выбирать только один из двух уровней математики: базовый или профильный. В этом году профильную математику планировали сдавать 55,2 % участников ГИА, базовую — 40 %. Однако последним не придется применить свои знания на практике: экзамен отменен.
Как заявила руководитель ФИПИ Оксана Решетникова, ЕГЭ по математике базового уровня в этом году проводиться не будет. Связано это с тем, что обязательный предмет проводился лишь для государственной итоговой аттестации, чтобы получить аттестат и оценку по математике.
Напомним, ранее Министерство просвещения РФ заявило, что ЕГЭ в этом году будут сдавать только те выпускники, которые планируют поступать в вуз. И экзамены будут только по тем предметам, которые нужны для поступления. Аттестат же будет выдан на основании текущих оценок.
Остается вопрос, состоится ли тогда самый массовый экзамен по русскому языку, который является обязательным. Его должны сдавать все 14,5 тысячи южноуральских выпускников этого года. Однако нужен он для поступления далеко не всем. Ранее федеральные власти предлагали провести экзамен в два дня, чтобы избежать большого скопления выпускников, но окончательного решения пока не приняли.
По-прежнему нет и расписания ЕГЭ. Ранее его старт планировали на 8 июня, однако теперь сроки перенесены на более поздний период.
Разделение ЕГЭ по математике на уровни улучшило результаты столичных школьников – глава МЦПМ
3 августа 2015 Москва ЕГЭРазделение Единого государственного экзамена по математике на базовый и профильный уровни улучшило результаты столичных школьников, сообщает Агентство городских новостей «Москва» со ссылкой на руководителя Федеральной комиссии разработчиков контрольных измерительных материалов (КИМ) ЕГЭ по математике, директора ГБОУ «Московский центр педагогического мастерства» Ивана Ященко.
«Уже видно, что в целом результаты ребят улучшились, и это очень хорошо заметно на волне честного ЕГЭ. Теперь мы можем говорить, что те цифры, которые есть, они действительно отражают уровень знаний ребят», — сказал Ященко.
По его словам, благодаря разделению ЕГЭ по математике существенно снизилась психологическая нагрузка на выпускников.
«Очень важно, что это было сделано очень мягко для выпускника, если кто-то что-то не понял, то можно сдать обе математики. Если ты выбрал по ошибке профильную математику, перепутав с базовой, и получил по ней «два», то на пересдачу можно было выбрать уровень. Это перестает создавать у ученика чувство математической ущербности», — подчеркнул директор.
ЕГЭ по математике с 2015 года разделен на два уровня – базовый и профильный. Базовый ЕГЭ сдают выпускники, которые идут на специальности, где математика не является профильным предметом или не планируют поступать в вузы. Профильный экзамен предназначен для тех выпускников, кого математика является одним из вступительных экзаменов в вуз.
Профильный экзамен предназначен для тех выпускников, кого математика является одним из вступительных экзаменов в вуз.
Базовый ЕГЭ включает в себя 20 заданий и оценивается по пятибалльной шкале.
Профильный экзамен состоит из двух частей и содержит 21 задание. Из них девять базового уровня, остальные повышенного и высокого. При этом 14 заданий требуют от ученика краткого вида в виде числа, дроби и так далее, в семи требуется развернутое решение. Чтобы сдать экзамен, надо набрать как минимум 27 баллов из 100. На выполнение заданий отводится четыре часа.
В конце июля пресс-центр Федеральной службы по надзору в сфере образования и науки сообщал, что Научно-методический совет по математике, созданный при Федеральном институте педагогических измерений признал эффективным разделение единого государственного экзамена по математике на базовый и профильный уровни.
Обязательными для всех выпускников являются два экзамена: русский язык и математика. Возможность сдачи ЕГЭ по математике на базовом или профильном уровне введена в 2015 году по предложению Ассоциации учителей и преподавателей.
Всего в этом году ЕГЭ по математике сдавали более 500 тысяч человек.
Успешная сдача экзамена базового уровня позволяет участникам подать документы в те вузы, где математика отсутствует в перечне вступительных испытаний, а профильного уровня — в вузы, где математика включена в перечень.
В России ЕГЭ служит одновременно как выпускной экзамен в школе и вступительный экзамен в вуз. Обязательными для получения аттестата об окончании российской школы являются ЕГЭ по русскому языку и математике, с 2020 года в число обязательных предметов для выпускников также планируется ввести иностранный язык.
Демоверсии ЕГЭ 2022 по математике
Утверждённые демоверсии ЕГЭ 2022 по математике от ФИПИ.Обновлено 10 ноября.
→ Демоверсия профильного уровня: math-demo2022-pro-v2.pdf
→ Демоверсия базового уровня: math-demo2022-b-v2.pdf
→ Спецификация профильного уровня: math-s2022-pro-v2.pdf
→ Спецификация базового уровня: math-s2022-b-v2.pdf
→ Кодификатор: math-k2022-v2. pdf
pdf
→ Скачать одним архивом: math-demo2022-v2.zip
1. Исключены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
2. Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
3. Внесено изменение в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
4. Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.
Изменения в КИМ ЕГЭ 2022 года базового уровня в сравнении с КИМ 2021 года1. Исключено задание 2, проверяющее умение выполнять вычисления и преобразования (данное требование внесено в позицию задачи 7 в новой нумерации).
2. Добавлены задание 5, проверяющее умение выполнять действия с геометрическими фигурами, и задание 20, проверяющее умение строить и исследовать простейшие математические модели.
3. Количество заданий увеличилось с 20 до 21, максимальный балл за выполнение всей работы стал равным 21.
Обобщенные планы вариантов КИМ ЕГЭ 2022 года по математике
|
№ |
Требования к уровню подготовки выпускников, проверяемому на ЕГЭ |
Уровень сложности задания |
Макс. |
Время выполнения (мин.) |
Время выполнения выпускником, изучавшим математику на профильном уровне (мин.) |
||
1 |
Уметь решать уравнения и неравенства | Б |
1 | 5 | 2 | ||
2 |
Уметь строить и исследовать простейшие математические модели |
Б |
1 | 5 | 2 | ||
3 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б |
1 | 5 | 3 | ||
4 |
Уметь выполнять вычисления и преобразования | Б |
1 | 5 | 3 | ||
5 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б |
1 | 10 | 3 | ||
6 |
Уметь выполнять действия с функциями | Б |
1 | 10 | 4 | ||
7 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
П |
1 | 15 | 6 | ||
8 |
Уметь строить и исследовать простейшие математические модели |
П |
1 | 15 | 7 | ||
9 |
Уметь выполнять действия с функциями | П |
1 | 15 | 8 | ||
| 10 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
П | 1 | 15 | 8 | ||
| 11 | Уметь выполнять действия с функциями | П | 1 | 15 | 9 | ||
| 12 | Уметь решать уравнения и неравенства | П | 2 | 20 | 10 | ||
| 13 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П | 3 | 40 | 20 | ||
| 14 | Уметь решать уравнения и неравенства | П | 2 | 30 | 15 | ||
| 15 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
П | 2 | 30 | 25 | ||
| 16 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П | 3 | – | 35 | ||
| 17 | Уметь решать уравнения и неравенства | В | 4 | – | 35 | ||
| 18 | Уметь строить и исследовать простейшие математические модели |
В | 4 | – | 40 | ||
Всего заданий – 18; из них Максимальный первичный балл за работу – 31. Общее время выполнения работы – 235 мин. |
|||||||
|
№ |
Требования к уровню подготовки выпускников, проверяемому на ЕГЭ |
Уровень сложности задания |
Макс. балл за выполнение задания |
Время выполнения (мин.) |
||
| 1 | Уметь выполнять вычисления и преобразования |
Б |
1 | 5 | ||
| 2 | Уметь выполнять вычисления и преобразования |
Б |
1 | 7 | ||
| 3 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
Б |
1 | 5 | ||
| 4 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
Б |
1 | 5 | ||
| 5 | Уметь выполнять действия с геометрическими фигурами |
Б |
1 | 6 | ||
| 6 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
Б |
1 | 8 | ||
| 7 | Уметь выполнять вычисления и преобразования |
Б |
1 | 7 | ||
| 8 | Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни |
Б |
1 | 4 | ||
| 9 | Уметь решать уравнения и неравенства |
Б |
1 | 7 | ||
| 10 | Уметь выполнять действия с геометрическими фигурами |
Б |
1 | 10 | ||
| 11 | Уметь строить и исследовать простейшие математические модели |
Б |
1 | 10 | ||
| 12 | Уметь строить и исследовать простейшие математические модели |
Б |
1 | 11 | ||
| 13 | Уметь выполнять действия с геометрическими фигурами |
Б | 1 | 11 | ||
| 14 | Уметь выполнять действия с функциями | Б | 1 | 7 | ||
| 15 | Уметь выполнять действия с геометрическими фигурами |
Б | 1 | 8 | ||
| 16 | Уметь выполнять действия с геометрическими фигурами |
Б | 1 | 8 | ||
| 17 | Уметь решать уравнения и неравенства |
Б | 1 | 8 | ||
| 18 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 8 | ||
| 19 | Уметь выполнять вычисления и преобразования |
Б | 1 | 15 | ||
| 20 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 15 | ||
| 21 | Уметь строить и исследовать простейшие математические модели |
Б | 1 | 15 | ||
| Всего заданий – 21; из них по типу заданий: с кратким ответом – 21; по уровню сложности: Б – 21.  Максимальный первичный балл за работу – 21. Общее время выполнения работы – 180 мин. |
||||||
Шкала перевода баллов по математике и другим предметам →
Какой ЕГЭ по математике выбрать: базу или профиль? | Поступи Онлайн
С 2019 года выпускники школ имеют право сдавать только один уровень ЕГЭ по математике — базовый или профильный. Разбираем, как принять правильное решение.
Кому нужна «база», а кому — «профиль»Главное, что вы должны запомнить: ЕГЭ по математике базового уровня и ЕГЭ по математике профильного уровня — это два совершенно разных экзамена. У них разная структура и, главное, разные цели.
Базовая математика — это обязательный экзамен. Сдать этот ЕГЭ должны все: без результатов по обязательным предметам (русский язык и математика базового уровня) вы просто не сможете получить аттестат.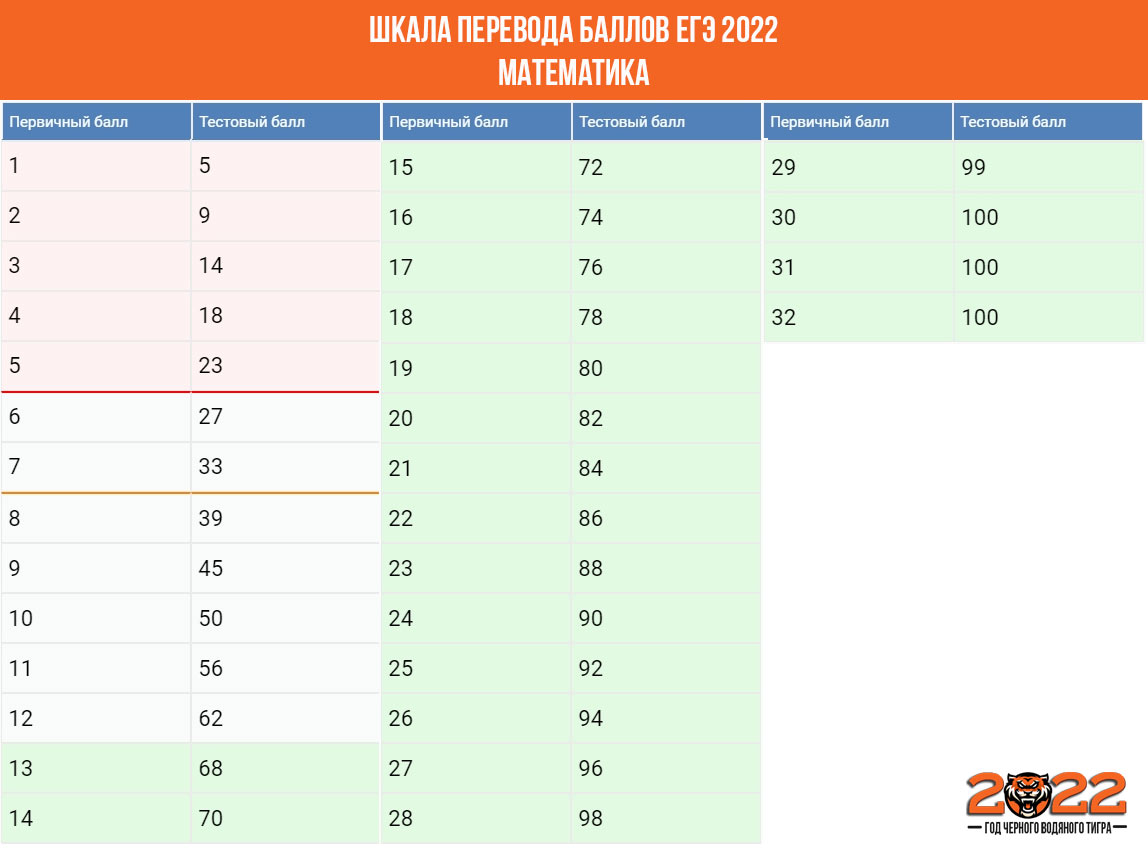 А без аттестата невозможно поступить в вуз. При этом результаты «базы» вузы не принимают. ЕГЭ по математике базового уровня — единственный в чистом виде «выпускной» экзамен.
А без аттестата невозможно поступить в вуз. При этом результаты «базы» вузы не принимают. ЕГЭ по математике базового уровня — единственный в чистом виде «выпускной» экзамен.
Если для поступления на специальности, которые вам интересны, нужно сдавать математику, это значит, что вы должны сдать ЕГЭ по профильной математике. Это уже экзамен по выбору, и вам нужно подать заявление на участие в нем до 1 февраля.
Если вы собираетесь поступать на гуманитарные специальности, вам точно не надо идти на ЕГЭ по математике профильного уровня. «Базу» вам нужно будет просто сдать с первого раза, чтобы получить свой аттестат летом, а не в сентябре, на пересдаче. Без аттестата вы просто не сможете принять участие в поступлении в вузы и пропустите приемную кампанию.
Тем, кто оказался в спорной ситуации и думает о разных специальностях (в том числе и о тех, где ЕГЭ по математике необходим), лучше сдавать профильный уровень. Так вы точно не упустите возможность поступить на специальность, где нужна профильная математика. Оцените свой уровень знаний и ответьте себе честно на вопрос: «Есть ли шансы, что я провалю „профиль“?». Если ответ — «да», то придется больше внимания уделить подготовке.
Так вы точно не упустите возможность поступить на специальность, где нужна профильная математика. Оцените свой уровень знаний и ответьте себе честно на вопрос: «Есть ли шансы, что я провалю „профиль“?». Если ответ — «да», то придется больше внимания уделить подготовке.
Раньше можно было сдавать и «базу», и профильную математику, но после введения новых правил выбрать оба уровня и сдать «для подстраховки» базовую не получится. Нужно выбрать что-то одно.
Чем отличаются друг от друга два экзамена по математикеВ ЕГЭ по математике базового уровня предусмотрено всего 20 заданий. Ответы на вопросы — числовые, либо в форме теста, где нужно выбрать правильный ответ. Заданий с развернутым ответом здесь нет. Экзамен оценивается по пятибалльной шкале, как в школе. Для того, чтобы этот ЕГЭ считался сданным, достаточно написать на тройку.
ЕГЭ по математике профильного уровня устроен иначе. Он делится на две части. Часть 1 похожа на экзамен по «базе», вот только заданий здесь — восемь. А в части 2 уже есть задания не только с коротким, но и с развернутым ответом. Это вопросы повышенной сложности, в том числе олимпиадного уровня. «Профиль», как и другие ЕГЭ, оценивается по стобалльной шкале. Чтобы сдать его, нужно перешагнуть порог в 27 баллов. Но чтобы участвовать в конкурсе в вузах, зачастую требуется куда более высокий результат.
Часть 1 похожа на экзамен по «базе», вот только заданий здесь — восемь. А в части 2 уже есть задания не только с коротким, но и с развернутым ответом. Это вопросы повышенной сложности, в том числе олимпиадного уровня. «Профиль», как и другие ЕГЭ, оценивается по стобалльной шкале. Чтобы сдать его, нужно перешагнуть порог в 27 баллов. Но чтобы участвовать в конкурсе в вузах, зачастую требуется куда более высокий результат.
Текст подготовила Наталия Киеня
(PDF) Тест по базовой математике позволяет предсказать статистические достижения и общую успеваемость за первый год обучения
Ссылки
Арум Р., Гаморан А. и Шавит Ю. (2007). Больше включения, чем отклонения: расширение, дифференциация и
структура рынка в сфере высшего образования. В Р. А. Я. Шавит и А. Гаморан (ред.), Стратификация в высшем образовании
: сравнительное исследование (стр. 1–35). Пало-Альто: Издательство Стэнфордского университета.
Баллард, С. Л., и Джонсон, М.Ф. (2004). Базовые математические навыки и успеваемость на вводном уроке экономики.
Л., и Джонсон, М.Ф. (2004). Базовые математические навыки и успеваемость на вводном уроке экономики.
Журнал экономического образования, 35 (1), 3–23. doi:10.3200/jece.35.1.3-23.
Будэ, Л., Ван Де Виль, М., Имбос, Т., Кандел, М., Броерс, Н., и Бергер, М. (2007). Достижения учащихся по курсу статистики
в отношении аспектов мотивации и поведения при учебе. Статистические исследования в области образования
Журнал, 6 (1), 5–21.
Бусато, В., Принс, Ф., Элсхаут, Дж., и Хамакер, К.(2000). Интеллектуальные способности, стиль обучения, личность,
мотивация достижения и академический успех студентов-психологов в высших учебных заведениях. Личность
и индивидуальные различия, 29, 1057–1068.
Кантильон, Б., Вербист, Г., и Сигал, И. (2005). Студентка в 21-й школе eeuw. Studiefinanciering voor het hoger
onderwijs во Фландерене. Связь с Onderwijskundig Beleids-en Praktijkgericht Wetenschappelijk
Onderzoek (OBPWO): Ministryie van de Vlaamse Gemeenschap, Departement Onderwijs.
Кашин, С., и Элмор, П. (2005). Исследование отношения к статистической шкале: исследование конструктивной валидности.
Образовательные и психологические измерения, 65(3), 509–524. дои: 10.1177/0013164404272488.
Кьези, Ф., и Прими, К. (2010). Когнитивные и некогнитивные факторы, связанные со статистическими достижениями учащихся.
Журнал статистических исследований в области образования, 9(1), 6–26.
Де Фрюйт, Ф., и Мервильде, И. (1996). Личность и интересы как предикторы потокового обучения и
достижений.Европейский журнал личности, 10, 405–425. doi:10.1002/(SICI)1099-0984(199612)
10:5<405::AID-PER255>3.0.CO;2-M.
Де Лаурентис, Г., Майно, Р., и Молтени, Л. (2010). Разработка, проверка и использование внутренних рейтингов:
методологий и тематических исследований. Западный Сассекс: Wiley Ltd.
Деклерк, К., и Вербовен, Ф. (2010). Slaagkansen aan vlaamse universiteiten: tijd om het beleid bij te sturen?
Импульс, 42(2), 88–98.
Образование во Фландрии.Широкий взгляд на фламандский образовательный ландшафт. (2008). Проверено 4 апреля 2013 г.
Элмор, П. Б., и Васу, Э. С. (1980). Взаимосвязь между выбранными переменными и достижением статистики: построение
теоретической модели. Журнал образования и психологии, 72 (4), 457–467. дои: 10.1037/0022-0663.72.4.457.
Филд, А. (2009). Обнаружение статистики с помощью SPSS. Лондон: Sage Publications Ltd.
Гал, И., и Гинзбург, Л. (1994). Роль убеждений и взглядов в обучении статистике: к оценке
рамки.Журнал статистического образования, 2 (2).
Галли, С., Кьези, Ф., и Прими, К. (2011). Измерение математических способностей, необходимых для «нематематических» специальностей:
построение шкалы с использованием IRT и дифференциальных элементов, функционирующих в образовательных контекстах.
Обучение и индивидуальные различия, 21(4), 392–402. doi:10.1016/j.lindif.2011.04.005.
Гарфилд, Дж., и Альгрен, А. (1988). Трудности в изучении основных понятий вероятности и статистики: последствия для исследований.Журнал исследований в области математического образования, 19 (1), 44–63.
(1988). Трудности в изучении основных понятий вероятности и статистики: последствия для исследований.Журнал исследований в области математического образования, 19 (1), 44–63.
Харлоу, Л., Буркхолдер, Г., и Морроу, Дж. (2002). Оценка отношений, навыков и производительности в учебном курсе
по расширенным количественным методам: подход к структурному моделированию. Моделирование структурными уравнениями: Многопрофильный журнал
, 9 (3), 413–430. doi: 10.1207/s15328007sem0903_6.
Джонсон, М., и Куеннен, Э. (2006). Базовые математические навыки и успеваемость в вводном курсе статистики.
Журнал статистического образования, 14(2).
Келчтерманс, С., и Вербовен, Ф. (2008). Участие и изучение решений в государственной системе высшего
образования. Журнал прикладной эконометрики, 25 (3), 335–391.
Кеннет Д., Янг А. М. и Катандзаро М. (2009). Переменные, способствующие успеху в учебе в промежуточном курсе статистики
: важность усвоенной находчивости. Педагог-психолог, 29(7),
Педагог-психолог, 29(7),
815–830.дои: 10.1080/014434105401.
Кунсель, Н., Хезлетт, С., и Онс, Д. (2004). Успеваемость в учебе, карьерный потенциал, креативность и профессиональная успеваемость
: может ли одна конструкция предсказать их все? Журнал личности и социальной психологии, 86 (1),
148–161. дои: 10.1037/0022-3514.86.1.148.
Лалонд Р. и Гарднер Р. (1993). Статистика как второй язык? Модель прогнозирования успеваемости
студентов-психологов. Канадский журнал поведенческих наук, 25 (1), 108–125.дои: 10.1037/h0078792.
Лаунсбери, Дж., Сандстром, Э., Лавленд, Дж., и Гибсон, Л. (2003). Интеллект, личностные качества «большой пятерки» и
трудолюбие служат предикторами конечной оценки. Личность и индивидуальные различия, 35, 1231–1239. дои: 10.
1016/s1475-1585(03)00053-5.
Махер, Д., Пехтер, М., Папоусек, И., и Руджери, К. (2011). Статистика тревожности, личностной тревожности, поведения при обучении,
и успеваемости. Европейский журнал психологии образования, 27(4), 483–498.doi: 10.1007/
Европейский журнал психологии образования, 27(4), 483–498.doi: 10.1007/
s10212-011-0090-5.
Л. Фонтейн и др.
| Цифровой репозиторий Католического университета Восточной Африки >
Элементы в DSpace защищены авторским правом, все права защищены, если не указано иное.
| ||||||||
Курсы – Математика
Нажмите, чтобы открыть PDF
Курс номер: математика 1
Pre-Calculus Единицы: 4
Класс:
Класс: 4 часа Лекция (GR)
Предварительная необходимость: Математика 203 или 211D
Допустимый для кредита: CSU, UC
Описание: Подготовка к последовательному исчислению или другим курсам, требующим хорошей алгебраической подготовки: неравенства, теория уравнений, последовательности и ряды, матрицы, функции и отношения, а также логарифмические и экспоненциальные функции; понятие функции, используемое как объединяющее понятие. 1701.00
1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Коллексный номер: Math 2
Precalculus с аналитической геометрией
единицы: 5
Класс: 5 часов Лекция (GR)
Предварительная необходимость: Математика 50 или 52C
приемлемый для кредита: CSU, UC
Описание: Высшая алгебра и аналитическая геометрия: линейные, квадратичные, полиномиальные, рациональные, экспоненциальные, логарифмические и обратные функции; определители, матрицы и линейные системы; нули многочленов, арифметические и геометрические прогрессии, математическая индукция; перестановки и комбинации, биномиальная теорема; векторы, конические сечения, перемещение и вращение осей, полярные координаты, линии и поверхности в пространстве, поверхности квадрика.1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Номер курса: МАТЕМАТИКА 3A
Исчисление I
Единицы: 5
Класс: 5 часов лекций (GR)
Предварительные требования: 90Math 242; или Math 1, и 50 или 52C
Принимается за кредит: CSU, UC
Описание: Теоремы о пределах и непрерывных функциях, производных, дифференциалах и приложениях: основные теоремы исчисления и приложения; свойства экспоненциальных, логарифмических и обратных тригонометрических функций, а также гиперболических функций. 1701.00
1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Номер курса: Math 3b
Calculus II
Unite: 5
класс: 5 часов Лекция (GR)
Предварительная необходимость: Math 3A
Приемлемые для кредита: CSU, UC
Описание: Применения определенного интеграла: методы интегрирования, полярные координаты, параметрические уравнения, бесконечные и степенные ряды. 1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Курс номер: Math 3C
Calculus III
единицы: 5
5
класс: 5 часов лекции (GR)
Предварительная необходимость: математика 3B
приемлемый для кредита: CSU, UC
Описание: Частичное дифференцирование: якобианы, преобразования, многократные интегралы, теоремы Грина и Стокса, дифференциальные формы, векторы и вектор-функции, геометрические координаты и векторное исчисление. 1701.00
1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Курс номер: Math 3D
Линейная алгебра и дифференциальные уравнения
Unite: 5
Класс: 5 часа Лекция (GR)
Предварительная необходимость: Math 3B
Math 3D эквивалентна математике 3Е плюс 3F.
Не засчитывается учащимся, которые завершили или в настоящее время зачислены на курс математики 3E или 3F.
Принимается за кредит: CSU, UC
Описание: Линейная алгебра и дифференциальные уравнения: обыкновенные дифференциальные уравнения, уравнения первого и второго порядка, однородные линейные дифференциальные уравнения, неоднородные линейные дифференциальные уравнения, метод преобразования Лапласа решений, решения бесконечных рядов и системы линейных дифференциальных уравнений.1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Курс номер: Math 13
Введение в статистику
единицы: 4
Класс: 4 часа Лекция (GR)
Предварительная необходимость: Математика 203 или 211D
Приемлемых для кредита: CSU, UC
Описание: Введение в теорию и практику статистики: сбор данных: выборочные, наблюдательные и экспериментальные исследования. Организация данных: одномерные и двумерные таблицы и графики, гистограммы.Описание данных: меры местоположения, распространения и корреляции. Теория: Вероятность, случайные величины, биномиальное и нормальное распределения. Выводы на основе данных: доверительные интервалы, проверка гипотез, z-тесты, t-тесты и тесты хи-квадрат; односторонний анализ отклонений. Регрессионные и непараметрические методы. 1701.00
Организация данных: одномерные и двумерные таблицы и графики, гистограммы.Описание данных: меры местоположения, распространения и корреляции. Теория: Вероятность, случайные величины, биномиальное и нормальное распределения. Выводы на основе данных: доверительные интервалы, проверка гипотез, z-тесты, t-тесты и тесты хи-квадрат; односторонний анализ отклонений. Регрессионные и непараметрические методы. 1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Курс номер: математика 15
Математика для либеральных искусств Студенты
единицы: 3
класс: 3 часа Лекция (GR)
Предварительная необходимость: Математика 203 или 211D
Приемлемых для кредита : CSU, UC
Описание: Фундаментальные идеи, лежащие в основе современной математики: элементы логики, множества и системы счисления; понятия элементарной алгебры, геометрии, топологии и комбинаторики. 1701.00
1701.00
AA/AS зона 4b; CSU район B4
Коллексный номер: Math 16A
Исчисление для бизнеса и жизни / социальных наук
единицы: 3
класс: 3 часа Лекция (GR)
Предварительная необходимость: Math 1 или 2
Допустимо для кредита: CSU, UC
Описание: Введение в аналитическую геометрию и дифференциальное и интегральное исчисление алгебраических функций с особым вниманием к простым приложениям.1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Курс номер: Math 16B
Исчисление для бизнеса и жизни / социальные науки
единицы: 3
класс: 3 часа Лекция (GR)
Предварительная необходимость: Math 16A или 3A
Приемлемо для кредита: CSU, UC
Описание: Продолжение дифференциального и интегрального исчисления: трансцендентные функции, методы интегрирования, частичное дифференцирование и множественное интегрирование с особым вниманием к приложениям. 1701.00
1701.00
AA/AS зона 4b; CSU область B4; ИГЭТК участок 2
Номер курса: MATH 48NA-TZ
Избранные темы по математике
Единицы: .5–5
Класс: 0–5 часов лекций, 0–15 часов P/NP лабораторных работ
Допустимо для кредита: CSU
Описание: См. раздел «Избранные темы». 1701.00
Номер курса: МАТЕМАТИКА 49
Самостоятельное изучение математики
Единицы: .5-5
Класс: (GR)
Курс обучения по этому разделу может повторяться три раза, максимум 5 единиц.
Допустимо для кредита: CSU
Описание: См. раздел о независимом исследовании. 1701.00
Коллексный номер: математика 50
Tragonometry единицы: 3
класс:
: 3 часа Лекция (GR)
Предварительная необходимость: Math 202, и 203 или 211D
не открыты для кредита студенты, которые завершили или в настоящее время зачислены в Math 52ABC.
Принимается за кредит: CSU
Описание: Введение в функциональную тригонометрию: основные определения, тождества, графики, обратные функции, тригонометрические уравнения и приложения, решение треугольников и приложения, полярные координаты, комплексные числа и теорема Муавра. 1701.00
AA/AS зона 4b; CSU район B4
Курс номер: Math 113
Математическая мастерская для статистики
единицы: 1
класс: 1 час Лекция (P / NP)
Предварительная необходимость: Математика 203 или 211D
Рекомендуемая подготовка: Математика 13 (рекомендуется сдавать одновременно)
Принимается за кредит: CSU
Описание: Закрепление навыков решения задач по статистике: Практикум по решению рутинных задач, связанных с теорией и практикой статистики; Сбор данных: выборочные, наблюдательные и экспериментальные исследования; Организация данных: одномерные и двумерные в таблицы и графики, гистограммы; Описание данных: меры местоположения, распространения и корреляции; Теория: вероятность, случайные величины, биномиальное и нормальное распределение; Выводы на основе данных: доверительные интервалы, проверка гипотез, z-тесты, t-тесты и тесты хи-квадрат, односторонний анализ дисперсий; а также регрессионные и непараметрические методы. 1701.00
1701.00
Курс номер: математика 201
Элементарная алгебра единицы: 4
класс: 5 часов лекции (GR)
Предварительная необходимость: Math 225 или 250 или 251D или 253 или соответствующее размещение через оценивание по нескольким параметрам
Не засчитывается учащимся, которые завершили или в настоящее время зачислены на курс Math 210ABCD.
Описание: Основные алгебраические операции: линейные уравнения и неравенства, отношения и функции, разложение квадратных многочленов на множители, решение квадратных уравнений, дроби, радикалы и показатели, задачи со словами, построение графиков и системы счисления.1701.00
Курс номер: Math 202
Геометрия
Геометрия
единицы: 3
класс: 3 часа Лекция (GR)
Предварительная необходимость: Математика 201 или 210D или соответствующее размещение через оценку нескольких мер
Описание: Введение в плоскостную геометрию с упором на математическую логику и доказательства: геометрические построения, конгруэнтные треугольники, параллельные прямые и параллелограммы, пропорции, подобные треугольники, окружности, многоугольники и площади. 1701.00
1701.00
AA/AS зона 4b
Курс номер: Math 203
Промежуточная алгебра единицы: 4
4
класс: 5 часов лекции (GR)
Предварительная необходимость: Math 201 или 210D или соответствующее размещение в рамках оценки нескольких мер
Рекомендуемая подготовка: Математика 202
Зачет не предоставляется учащимся, которые завершили или в настоящее время зачислены на курс математики 211ABCD.
Имеет право на зачет по результатам экзамена.
Описание: Промежуточные алгебраические операции: свойства и операции действительных чисел; решения и графики линейных уравнений с одной и двумя переменными; уравнения абсолютного значения; расширенный факторинг; комплексные числа; квадратные уравнения и системы квадратных уравнений; коники; определители; решения и графики первой степени, квадратичных и рациональных неравенств; экспоненциальные и логарифмические функции; и последовательности и серии. 1701.00
1701.00
AA/AS зона 4b
Номер курса: MATH 248NA-TZ
Избранные темы по математике
Единицы: .5–5
Класс: 0–5 часов лекций, 0–15 часов лабораторных занятий (GR или P/NP)
Описание: См. раздел «Избранные темы». 1701.00
Номер курса: МАТЕМАТИКА 250
Арифметика
Единицы: 3
Класс: 3 часа лекций (GR)
Без присвоения степени
Описание: Курс повышения квалификации по основным процессам арифметики: целые числа, дроби, десятичные дроби и проценты; метрическая система введена и включена в арифметический материал.4930.41
Номер курса: Math 253
Pre-Algebra единицы: 3
класс: 3 часа Лекция (GR)
Рекомендуемая подготовка: Математика 250 или 251D или соответствующее размещение через оценку нескольких мер
Без присвоения степени
Описание: Основы предварительной алгебры: свойства действительных чисел, разложение на множители и кратные, отношение и пропорция, числа со знаком, линейные уравнения и формулы, степени и корни, проценты и средние значения, английские и метрические измерения . 4930.41
4930.41
Курс номер: Math 270
Математическая мастерская для арифметика
единицы: 1
Класс: 1 час Лекция (P / NP)
Рекомендуемая подготовка: Математика 250 (рекомендуется принимать одновременно)
Без присвоения степени
Описание: Укрепление навыков решения задач по арифметике: Практикум по решению рутинных задач, связанных с целыми числами и арифметическими операциями, дробями, десятичными дробями, отношениями, пропорциями, процентами, измерениями и шкалами, интерпретацией обозначений, и простые уравнения и формулы.4930.41
Номер курса: МАТЕМАТИКА 271
Семинар по математике для предварительной алгебры
Единицы: 1
Класс: 1 час лекции (P/NP)
9024 Рекомендуемая многократная подготовка или размещение: по 510 Math -оценка мер; и математика 253 (рекомендуется сдавать одновременно)
Неприменимо к ученой степени
Описание: Укрепление навыков решения задач по предварительной алгебре: Семинар по решению рутинных задач, связанных с действительными числами, факторингом и кратными, отношениями и пропорциями, со знаком числа, линейные уравнения и формулы, степени и корни, проценты и средние значения, английские и метрические измерения. 4930.41
4930.41
Курс номер: Math 272
Математический мастерский мастерской для элементарной алгебры
единицы: 1
класс: 1 час Лекция (P / NP)
Предварительная необходимость: Math 250 или 251D или 225 или 295 253 или соответствующее размещение посредством оценивания по нескольким параметрам
Рекомендуемая подготовка: Математика 201 (рекомендуется сдавать одновременно)
Неприменимо к ученой степени
Описание: Укрепление навыков решения задач по элементарной алгебре: Семинар по решению рутинных задач с основными алгебраическими операциями, линейными уравнениями и неравенствами, отношениями и функциями, факторингом квадратных многочленов, решением квадратных уравнений, дробей, радикалов и показателей, задачами со словами, а также графическими и числовыми системами.1701.00
Курс номер: Math 273
Математическая мастерская для промежуточной алгебры
единицы: 1
класс: 1 час Лекция (P / NP)
Предварительная необходимость: Math 201 или 210D или соответствующее размещение посредством оценки по нескольким параметрам
Рекомендуемая подготовка: Math 202; и математика 203 (рекомендуется сдавать одновременно)
Не требует присвоения степени
Описание: Укрепление навыков решения задач по алгебре среднего уровня: мастер-класс по решению рутинных задач, связанных со свойствами вещественных чисел и операциями, решениями и графиками линейных уравнений в одна и две переменные; уравнения с абсолютными значениями, расширенный факторинг, комплексные числа, квадратные уравнения и системы квадратных уравнений, конические сечения, определители; решения и графики первой степени, квадратные и рациональные неравенства; экспоненциальные и логарифмические функции, а также последовательности и ряды. 1701.00
1701.00
Номер курса: MATH 348NA-TZ
Избранные темы по математике
Единицы: .5–5
Класс: 0–5 часов лекций, 0–15 часов лабораторных работ (GR или P/NP)
Неприменимо к степени
Описание: См. раздел «Выбранные темы». 4930.40
— Весна 2022 г. — Факультет математики
Основная цель этого курса — служить подготовкой к МАТЕМАТИКЕ 105, МАТЕМАТИКЕ 106, МАТЕМАТИКЕ 107 и МАТЕМАТИКЕ 112 с упором на методы решения задач и графические технологии.Содержание включает следующие темы: линейные, квадратичные, полиномиальные, рациональные и абсолютные уравнения и неравенства, алгебраические выражения, методы построения графиков, методы факторинга, показатели и анализ основных данных. Студенты, желающие продолжить изучение математических курсов более высокого уровня, смогут работать с дополнительными учебными материалами по алгебре и тригонометрии, чтобы облегчить эту подготовку. Этот курс сам по себе не может быть использован для удовлетворения базовых требований по математике для какой-либо программы на получение степени.Экзамены проходят под наблюдением.
Этот курс сам по себе не может быть использован для удовлетворения базовых требований по математике для какой-либо программы на получение степени.Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 100-001 | Пн | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-002 | Пн | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-003 | Пн | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-004 | Пн | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-005 | Пн | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-006 | Пн | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-007 | Пн | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-008 | Пн | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-009 | Ту | 8:00–9:15 | Онлайн |
| МАТЕМАТИКА 100-010 | Ту | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-011 | Ту | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-012 | Ту | 9:30–10:45 | Онлайн |
| МАТЕМАТИКА 100-013 | Ту | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-014 | Ту | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-015 | Ту | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-016 | Ту | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-017 | Ту | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-018 | Ту | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-021 | Ту | 11:00-12:15 | Онлайн |
| МАТЕМАТИКА 100-025 | Ту | 12:30-13:45 | Онлайн |
| МАТЕМАТИКА 100-029 | Ту | 14:00–15:15 | Онлайн |
| МАТЕМАТИКА 100-103 | Онлайн | ||
| МАТЕМАТИКА 100-201 | Онлайн | ||
| МАТЕМАТИКА 100-202 | Онлайн | ||
| МАТЕМАТИКА 100-203 | Онлайн | ||
| МАТЕМАТИКА 100-401 | Онлайн | ||
| МАТЕМАТИКА 100-402 | Онлайн | ||
| МАТЕМАТИКА 100-403 | Онлайн |
Этот курс исследует алгебраическое мышление от раннего детства до средней школы, уделяя особое внимание различным концепциям алгебры, включая обобщенную арифметику; узоры и функции; и моделирование. Студенты изучат различные темы алгебры K-8 с продвинутой точки зрения. Экзамены проходят под наблюдением.
Студенты изучат различные темы алгебры K-8 с продвинутой точки зрения. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 106-001 | Пн, Ср, Пт | 10:00–10:50 | ОБЕД 353 |
Основная цель этого курса — помочь учащимся понять, интерпретировать и представить данные полезным способом, чтобы подготовить студентов к курсам по статистике.Курс предоставит студентам знания основных математических и программных инструментов и концепций, которые они могут использовать для интерпретации количественной информации, с которой они сталкиваются в своей повседневной жизни. Благодаря полученным знаниям студенты смогут лучше понимать и оценивать достоверность количественной информации, которую они получают через Интернет, газеты, телевидение и т. д. Темы курса будут включать создание различных сводок данных и описательной статистики, вероятность, нормальное распределение, линейное и другие модели регрессии, применяющие методы к наборам данных реального мира.Экзамены проходят под наблюдением.
Благодаря полученным знаниям студенты смогут лучше понимать и оценивать достоверность количественной информации, которую они получают через Интернет, газеты, телевидение и т. д. Темы курса будут включать создание различных сводок данных и описательной статистики, вероятность, нормальное распределение, линейное и другие модели регрессии, применяющие методы к наборам данных реального мира.Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 107-001 | Вт, Чт | 8:00–9:15 | САГХА 101 |
| МАТЕМАТИКА 107-002 | Вт, Чт | 8:00–9:15 | САГХА 202 |
| МАТЕМАТИКА 107-003 | Вт, Чт | 11:00-12:15 | САГХА 202 |
| МАТЕМАТИКА 107-004 | Вт, Чт | 12:30-13:45 | САГХА 202 |
| МАТЕМАТИКА 107-005 | Вт, Чт | 14:00–15:15 | САГХА 101 |
| МАТЕМАТИКА 107-006 | Вт, Чт | 15:30-16:45 | САГХА 101 |
| МАТЕМАТИКА 107-102 | Онлайн | ||
| МАТЕМАТИКА 107-202 | Онлайн | ||
| МАТЕМАТИКА 107-402 | Онлайн |
Основная цель этого курса — помочь учащимся использовать алгебраические и тригонометрические функции для моделирования ситуаций из реальной жизни. Особое внимание будет уделено приложениям, относящимся к специальностям «Архитектура и речь», «Язык» и «Науки о слухе». Темы курса будут включать отношения и пропорции, функции и графики, линейные и квадратичные функции и уравнения, тригонометрические функции и уравнения, подбор синусоидальных кривых, экспоненциальные и логарифмические функции и уравнения, все с упором на приложения. Экзамены проходят под наблюдением.
Особое внимание будет уделено приложениям, относящимся к специальностям «Архитектура и речь», «Язык» и «Науки о слухе». Темы курса будут включать отношения и пропорции, функции и графики, линейные и квадратичные функции и уравнения, тригонометрические функции и уравнения, подбор синусоидальных кривых, экспоненциальные и логарифмические функции и уравнения, все с упором на приложения. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 108-001 | Пн, Вт, Ср, Чт | 13:00–13:50 | САГХА 101 |
| МАТЕМАТИКА 108-002 | Пн, Вт, Ср, Чт | 17:00-17:50 | МЛЦ 125 |
Темы включают свойства функций и графиков, линейные и квадратные уравнения, полиномиальные функции, экспоненциальные и логарифмические функции с приложениями. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 112-001 | Пн, Ср, Пт | 10:00–10:50 | МЛНГ 310 |
| МАТЕМАТИКА 112-002 | Пн, Ср, Пт | 8:00–8:50 | МЛНГ 311 |
| МАТЕМАТИКА 112-003 | Пн, Ср, Пт | 8:00–8:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-004 | Пн, Ср, Пт | 9:00–9:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-005 | Пн, Ср, Пт | 9:00–9:50 | МЛЦ 119 |
| МАТЕМАТИКА 112-006 | Пн, Ср, Пт | 10:00–10:50 | МЛЦ 119 |
| МАТЕМАТИКА 112-007 | Пн, Ср, Пт | 10:00–10:50 | ГНИЦ 206 |
| МАТЕМАТИКА 112-008 | Пн, Ср, Пт | 10:00–10:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-009 | Пн, Ср, Пт | 11:00-11:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-010 | Пн, Ср, Пт | 11:00-11:50 | ГНИЦ 206 |
| МАТЕМАТИКА 112-011 | Пн, Ср, Пт | 12:00-12:50 | ХАРВ 404 |
| МАТЕМАТИКА 112-012 | Пн, Ср, Пт | 12:00-12:50 | САГХА 101 |
| МАТЕМАТИКА 112-013 | Пн, Ср, Пт | 12:00-12:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-014 | Пн, Ср, Пт | 13:00–13:50 | ХАРВ 404 |
| МАТЕМАТИКА 112-015 | Пн, Ср, Пт | 13:00–13:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-016 | Пн, Ср, Пт | 14:00–14:50 | ХАРВ 404 |
| МАТЕМАТИКА 112-017 | Пн, Ср, Пт | 14:00–14:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-018 | Пн, Ср, Пт | 15:00–15:50 | ГНИЦ 206 |
| МАТЕМАТИКА 112-019 | Пн, Ср, Пт | 15:00–15:50 | МЛЦ 125 |
| МАТЕМАТИКА 112-020 | Пн, Ср, Пт | 15:00–15:50 | ХАРВ 404 |
| МАТЕМАТИКА 112-022 | Пн, Ср | 16:00–17:15 | МЛЦ 119 |
| МАТЕМАТИКА 112-023 | Пн, Ср, Пт | 13:00–13:50 | САГХА 202 |
| МАТЕМАТИКА 112-024 | Пн, Ср, Пт | 14:00–14:50 | САГХА 101 |
| МАТЕМАТИКА 112-025 | Пн, Ср, Пт | 15:00–15:50 | ШНТЗ 247 |
| МАТЕМАТИКА 112-027 | Пн, Ср | 16:00–17:15 | ПСИХИЧЕСКИЙ 306 |
| МАТЕМАТИКА 112-101 | Онлайн | ||
| МАТЕМАТИКА 112-102 | Онлайн | ||
| МАТЕМАТИКА 112-103 | Онлайн | ||
| МАТЕМАТИКА 112-201 | Онлайн | ||
| МАТЕМАТИКА 112-202 | Онлайн | ||
| МАТЕМАТИКА 112-203 | Онлайн | ||
| МАТЕМАТИКА 112-401 | Онлайн | ||
| МАТЕМАТИКА 112-402 | Онлайн | ||
| МАТЕМАТИКА 112-403 | Онлайн |
Введение в дифференциальное и интегральное исчисление. Студенты должны иметь графический калькулятор. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Студенты должны иметь графический калькулятор. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 113-001 | Вт, Чт | 8:00–9:15 | ЦЕСЛ 102 |
| МАТЕМАТИКА 113-103 | Онлайн | ||
| МАТЕМАТИКА 113-203 | Онлайн | ||
| МАТЕМАТИКА 113-403 | Онлайн |
Вводные темы в дифференциальное и интегральное исчисление с особым акцентом на понимание основных концепций и их приложений в бизнесе. Microsoft Excel и графические калькуляторы будут использоваться в качестве инструментов для дальнейшего понимания этих концепций. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса.
Microsoft Excel и графические калькуляторы будут использоваться в качестве инструментов для дальнейшего понимания этих концепций. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 116-001 | Пн, Ср, Пт | 9:00–9:50 | ОБЕД 337 |
| МАТЕМАТИКА 116-002 | Пн, Ср, Пт | 9:00–9:50 | ЧВЭЗ 303 |
| МАТЕМАТИКА 116-003 | Пн, Ср, Пт | 10:00–10:50 | ЧВЭЗ 303 |
| МАТЕМАТИКА 116-004 | Пн, Ср, Пт | 10:00–10:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-005 | Пн, Ср, Пт | 12:00-12:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-006 | Пн, Ср, Пт | 13:00–13:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-007 | Пн, Ср, Пт | 14:00–14:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-009 | Вт, Чт | 8:00–9:15 | ЭДУК 240 |
| МАТЕМАТИКА 116-010 | Вт, Чт | 9:30–10:45 | ЭДУК 240 |
| МАТЕМАТИКА 116-011 | Вт, Чт | 12:30-13:45 | САГХА 114 |
| МАТЕМАТИКА 116-012 | Вт, Чт | 12:30-13:45 | ХАРВ 301 |
| МАТЕМАТИКА 116-013 | Вт, Чт | 14:00–15:15 | ГНИЦ 222 |
| МАТЕМАТИКА 116-015 | Пн, Ср, Пт | 12:00-12:50 | ХАРВ 411 |
| МАТЕМАТИКА 116-017 | Пн, Ср, Пт | 8:00–8:50 | ПСИХИК 206 |
| МАТЕМАТИКА 116-018 | Пн, Ср | 16:00–17:15 | ПСИХИК 206 |
| МАТЕМАТИКА 116-019 | Пн, Ср, Пт | 9:00–9:50 | ПСИХИК 206 |
| МАТЕМАТИКА 116-020 | Пн, Ср, Пт | 15:00–15:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-021 | Пн, Ср, Пт | 9:00–9:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 116-022 | Пн, Ср, Пт | 10:00–10:50 | МЛНГ 411 |
| МАТЕМАТИКА 116-023 | Пн, Ср, Пт | 11:00-11:50 | ЭДУК 310 |
| МАТЕМАТИКА 116-101 | Онлайн | ||
| МАТЕМАТИКА 116-201 | Онлайн | ||
| МАТЕМАТИКА 116-401 | Онлайн |
Курс с использованием реальных примеров разработки и изучения моделей биологических динамических систем с использованием концепций исчисления. Студенты, изучающие этот курс, узнают, как интерпретировать и разрабатывать основанные на исчислении модели биологических систем, которые описывают изменение величин в реалистичных и соответствующих условиях, взятых из физиологии, неврологии, экологии и эволюции. Они также изучат основы языка программирования, достаточного для построения графиков функций, данных и моделирования систем дифференциальных уравнений. Этот курс предназначен для студентов биологических наук или тех, кто заинтересован в карьере в медицине, и не требует каких-либо предварительных знаний в области исчисления или программирования.
Студенты, изучающие этот курс, узнают, как интерпретировать и разрабатывать основанные на исчислении модели биологических систем, которые описывают изменение величин в реалистичных и соответствующих условиях, взятых из физиологии, неврологии, экологии и эволюции. Они также изучат основы языка программирования, достаточного для построения графиков функций, данных и моделирования систем дифференциальных уравнений. Этот курс предназначен для студентов биологических наук или тех, кто заинтересован в карьере в медицине, и не требует каких-либо предварительных знаний в области исчисления или программирования.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 119A-001 | Пн, Ср | 16:00–17:15 | БИОВ 301 |
| МАТЕМАТИКА 119A-001A | Чт | 12:00-12:50 | САГХА 101 |
| МАТЕМАТИКА 119A-001B | Чт | 15:00–15:50 | САГХА 225 |
Обзор алгебры и тригонометрии; изучение функций, включая полиномиальные, рациональные, экспоненциальные, логарифмические и тригонометрические. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Для учащихся, которые имеют кредит в средней школе по алгебре и тригонометрии в колледже, но не набрали достаточного количества баллов на вступительном тесте UA по математике, чтобы войти в исчисление. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня.Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Для учащихся, которые имеют кредит в средней школе по алгебре и тригонометрии в колледже, но не набрали достаточного количества баллов на вступительном тесте UA по математике, чтобы войти в исчисление. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня.Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 120R-001 | Пн, Вт, Ср, Чт, Пт | 8:00–8:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-002 | Пн, Вт, Ср, Чт, Пт | 8:00–8:50 | МЛЦ 141 |
| МАТЕМАТИКА 120R-003 | Пн, Вт, Ср, Чт, Пт | 9:00–9:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-004 | Пн, Вт, Ср, Чт, Пт | 9:00–9:50 | ПСИХИК 307 |
| МАТЕМАТИКА 120R-005 | Пн, Вт, Ср, Чт, Пт | 10:00–10:50 | ПСИХИК 204 |
| МАТЕМАТИКА 120R-006 | Пн, Вт, Ср, Чт, Пт | 10:00–10:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-007 | Пн, Вт, Ср, Чт, Пт | 11:00-11:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-008 | Пн, Вт, Ср, Чт, Пт | 11:00-11:50 | ПСИХИК 205 |
| МАТЕМАТИКА 120R-009 | Пн, Вт, Ср, Чт, Пт | 12:00-12:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-010 | Пн, Вт, Ср, Чт, Пт | 13:00–13:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-011 | Пн, Вт, Ср, Чт, Пт | 13:00–13:50 | ПСИХИК 205 |
| МАТЕМАТИКА 120R-012 | Пн, Вт, Ср, Чт, Пт | 14:00–14:50 | ОБЕД 318 |
| МАТЕМАТИКА 120R-013 | Пн, Вт, Ср, Чт, Пт | 14:00–14:50 | ПСИХИК 205 |
| МАТЕМАТИКА 120R-014 | Пн, Вт, Ср, Чт, Пт | 15:00–15:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 120R-015 | Пн, Вт, Ср, Чт, Пт | 15:00–15:50 | ОБЕД 318 |
| МАТЕМАТИКА 120R-016 | Пн, Вт, Ср, Чт | 16:00–17:05 | ПСИХИК 204 |
| МАТЕМАТИКА 120R-017 | Пн, Вт, Ср, Чт | 16:00–17:05 | ПСИХИК 307 |
| МАТЕМАТИКА 120R-019 | Пн, Вт, Ср, Чт | 17:15-18:20 | ПСИХИК 204 |
| МАТЕМАТИКА 120R-102 | Онлайн | ||
| МАТЕМАТИКА 120R-103 | Онлайн | ||
| МАТЕМАТИКА 120R-104 | Онлайн | ||
| МАТЕМАТИКА 120R-202 | Онлайн | ||
| МАТЕМАТИКА 120R-203 | Онлайн | ||
| МАТЕМАТИКА 120R-204 | Онлайн | ||
| МАТЕМАТИКА 120R-402 | Онлайн | ||
| МАТЕМАТИКА 120R-403 | Онлайн |
Элементарные функции, их свойства и использование в моделировании. Для этого курса необходим графический калькулятор. Мы рекомендуем
Модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя.
Для этого курса необходим графический калькулятор. Мы рекомендуем
Модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 122A-101 | Онлайн | ||
| МАТЕМАТИКА 122A-201 | Онлайн | ||
| МАТЕМАТИКА 122A-401 | Онлайн |
Введение в исчисление в первом семестре для студентов технических специальностей, естественных наук и математики, от скорости изменений до интеграции, с акцентом на понимание, решение проблем и моделирование. Рассматриваемые темы включают ключевые понятия производной и определенного интеграла, методы дифференцирования и приложения с использованием алгебраических и трансцендентных функций. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Экзамены проходят под наблюдением. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня.Такие студенты могут быть исключены из курса.
Рассматриваемые темы включают ключевые понятия производной и определенного интеграла, методы дифференцирования и приложения с использованием алгебраических и трансцендентных функций. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Экзамены проходят под наблюдением. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня.Такие студенты могут быть исключены из курса.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 122B-001 | Пн, Вт, Ср, Чт, Пт | 8:00–8:50 | ПСИХИК 307 |
| МАТЕМАТИКА 122B-003 | Пн, Вт, Ср, Чт, Пт | 9:00–9:50 | ПСИХИК 204 |
| МАТЕМАТИКА 122B-004 | Пн, Вт, Ср, Чт, Пт | 9:00–9:50 | ПСИХИК 205 |
| МАТЕМАТИКА 122B-005 | Пн, Вт, Ср, Чт, Пт | 12:00-12:50 | ПСИХИК 205 |
| МАТЕМАТИКА 122B-006 | Пн, Вт, Ср, Чт, Пт | 14:00–14:50 | БИОВ 219 |
| МАТЕМАТИКА 122B-007 | Пн, Вт, Ср, Чт, Пт | 11:00-11:50 | ПСИХИК 204 |
| МАТЕМАТИКА 122B-008 | Пн, Вт, Ср, Чт, Пт | 11:00-11:50 | САГХА 101 |
| МАТЕМАТИКА 122B-009 | Пн, Вт, Ср, Чт, Пт | 12:00-12:50 | ПСИХИК 204 |
| МАТЕМАТИКА 122B-011 | Пн, Вт, Ср, Чт, Пт | 13:00–13:50 | САГХА 225 |
| МАТЕМАТИКА 122B-012 | Пн, Вт, Ср, Чт, Пт | 14:00–14:50 | САГХА 225 |
| МАТЕМАТИКА 122B-013 | Пн, Вт, Ср, Чт, Пт | 14:00–14:50 | МАТЕМАТИКА 401 |
| МАТЕМАТИКА 122B-015 | Пн, Вт, Ср, Чт, Пт | 15:00–15:50 | ПСИХИК 307 |
| МАТЕМАТИКА 122B-016 | Пн, Вт, Ср, Чт | 16:00–17:05 | СВЯЗЬ 311 |
| МАТЕМАТИКА 122B-102 | Онлайн | ||
| МАТЕМАТИКА 122B-202 | Онлайн | ||
| МАТЕМАТИКА 122B-402 | Онлайн |
Ускоренная версия MATH 122B. Введение в исчисление с упором на понимание и решение проблем. Понятия представлены графически и численно, а также алгебраически. Элементарные функции, их свойства и использование в моделировании; основные понятия производной и определенного интеграла; методы дифференцирования, использующие производную для понимания поведения функций; приложения к задачам оптимизации в физике, биологии и экономике. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84.Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Введение в исчисление с упором на понимание и решение проблем. Понятия представлены графически и численно, а также алгебраически. Элементарные функции, их свойства и использование в моделировании; основные понятия производной и определенного интеграла; методы дифференцирования, использующие производную для понимания поведения функций; приложения к задачам оптимизации в физике, биологии и экономике. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84.Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 125-103 | Онлайн | ||
| МАТЕМАТИКА 125-203 | Онлайн | ||
| МАТЕМАТИКА 125-403 | Онлайн |
Продолжение МАТЕМАТИКА 122B или МАТЕМАТИКА 125. Методы символьного и численного интегрирования, приложения определенного интеграла к геометрии, физике, экономике и вероятности; дифференциальные уравнения с численной, графической и алгебраической точек зрения; моделирование с помощью дифференциальных уравнений, аппроксимации рядами Тейлора. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Экзамены проходят под наблюдением.
Методы символьного и численного интегрирования, приложения определенного интеграла к геометрии, физике, экономике и вероятности; дифференциальные уравнения с численной, графической и алгебраической точек зрения; моделирование с помощью дифференциальных уравнений, аппроксимации рядами Тейлора. Для этого курса необходим графический калькулятор. Мы рекомендуем модели TI-83 или TI-84. Калькуляторы, выполняющие символьные операции, такие как TI-89, NSpire CAS или HP50g, использовать нельзя. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 129-001 | Пн, Ср, Пт | 8:00–8:50 | БИОВ 237 |
| МАТЕМАТИКА 129-003 | Пн, Ср, Пт | 9:00–9:50 | БИОВ 237 |
| МАТЕМАТИКА 129-005 | Пн, Ср, Пт | 10:00–10:50 | БИОВ 237 |
| МАТЕМАТИКА 129-006 | Пн, Ср, Пт | 11:00-11:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 129-007H | Пн, Ср, Пт | 11:00-11:50 | БИОВ 237 |
| МАТЕМАТИКА 129-008 | Пн, Ср, Пт | 12:00-12:50 | БИОВ 237 |
| МАТЕМАТИКА 129-009 | Пн, Ср, Пт | 13:00–13:50 | БИОВ 219 |
| МАТЕМАТИКА 129-010 | Пн, Ср, Пт | 13:00–13:50 | ЧВЭЗ 104 |
| МАТЕМАТИКА 129-011 | Пн, Ср, Пт | 14:00–14:50 | БИОВ 237 |
| МАТЕМАТИКА 129-012 | Пн, Ср, Пт | 14:00–14:50 | ХАРВ 411 |
| МАТЕМАТИКА 129-014 | Вт, Чт | 15:30-16:45 | ЧВЭЗ 104 |
| МАТЕМАТИКА 129-015 | Вт, Чт | 9:30–10:45 | ЧВЭЗ 316 |
| МАТЕМАТИКА 129-017 | Вт, Чт | 11:00-12:15 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 129-018 | Вт, Чт | 12:30-13:45 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 129-019 | Пн, Ср, Пт | 9:00–9:50 | БИОВ 219 |
| МАТЕМАТИКА 129-020 | Вт, Чт | 14:00–15:15 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 129-103 | Онлайн | ||
| МАТЕМАТИКА 129-203 | Онлайн | ||
| МАТЕМАТИКА 129-403 | Онлайн |
Организация данных: отображение распределений, показателей центра, показателей распространения, диаграмм рассеяния, корреляции, регрессии и их интерпретации. План экспериментов: простые случайные выборки и их выборочное распределение, модели вероятности, нормального распределения и нормального приближения. Статистический вывод: доверительные интервалы и проверка гипотез, t-процедуры и тесты хи-квадрат. Не предназначено для тех, кто планирует дальнейшее изучение статистики. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса.Экзамены проходят под наблюдением.
План экспериментов: простые случайные выборки и их выборочное распределение, модели вероятности, нормального распределения и нормального приближения. Статистический вывод: доверительные интервалы и проверка гипотез, t-процедуры и тесты хи-квадрат. Не предназначено для тех, кто планирует дальнейшее изучение статистики. За исключением случаев, предусмотренных политикой университета в отношении повторения курса, зачет по этому курсу не засчитывается, если студент имеет зачет по математическому курсу более высокого уровня. Такие студенты могут быть исключены из курса.Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 163-001 | Вт, Чт | 8:00–9:15 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 163-002 | Вт, Чт | 9:30–10:45 | ЧВЭЗ 104 |
| МАТЕМАТИКА 163-003 | Вт, Чт | 15:30-16:45 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 163-004 | Вт, Чт | 12:30-13:45 | ХАРВ 428 |
| МАТЕМАТИКА 163-005 | Вт, Чт | 9:30–10:45 | МЛНГ 410 |
| МАТЕМАТИКА 163-006 | Вт, Чт | 14:00–15:15 | МЛНГ 410 |
ДАННЫЕ 195M: Основной коллоквиум по математике и SDS
Курс в стиле семинара, предназначенный для ознакомления математического сообщества со специальностями факультета математики в целом, поддержки новых специальностей по мере их адаптации к университетской жизни и ожиданиям, а также для развития у студентов навыков письменного и устного общения, особенно по темам, связанным с математикой.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 195M-001 | Пн | 15:00–15:50 | МТЛ 124 |
МАТЕМАТИКА 195M: основной коллоквиум по математике и SDS
Курс в стиле семинара, предназначенный для ознакомления математического сообщества со специальностями факультета математики в целом, поддержки новых специальностей по мере их адаптации к университетской жизни и ожиданиям, а также для развития у студентов навыков письменного и устного общения, особенно по темам, связанным с математикой.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 195M-001 | Пн | 15:00–15:50 | МТЛ 124 |
МАТЕМАТИКА 196A: Репетиторство в школах
Этот курс предназначен для ознакомления математически талантливых студентов колледжей с профессией учителя математики. Учащимся предоставляется возможность наблюдать и преподавать на уроках математики в средних и старших классах. Кроме того, время занятий будет посвящено разработке методов репетитора, изучению стилей обучения и изучению различных методов обучения. Чтение, размышления, обсуждения и групповая работа облегчат учащимся понимание преподавания и изучения математики. При подаче заявления предпочтение отдается учащимся с уровнем подготовки по математике или выше
Учащимся предоставляется возможность наблюдать и преподавать на уроках математики в средних и старших классах. Кроме того, время занятий будет посвящено разработке методов репетитора, изучению стилей обучения и изучению различных методов обучения. Чтение, размышления, обсуждения и групповая работа облегчат учащимся понимание преподавания и изучения математики. При подаче заявления предпочтение отдается учащимся с уровнем подготовки по математике или выше
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 196A-001 | Ср | 16:00–16:50 | ПАС 588 |
МАТЕМАТИКА 196L: семинар по дополнительным инструкциям по предварительному исчислению
Этот курс разработан как дополнение к MATH 120R. Учащиеся, зачисленные на курс, будут участвовать в еженедельном занятии, относящемся к материалу, описанному в MATH 120R. Требуется одновременная регистрация в MATH 120R.
Учащиеся, зачисленные на курс, будут участвовать в еженедельном занятии, относящемся к материалу, описанному в MATH 120R. Требуется одновременная регистрация в MATH 120R.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 196L-001 | Пн | 16:00–17:50 | МТЛ 124 |
| МАТЕМАТИКА 196L-002 | Чт | 14:00–15:50 | МТЛ 123 |
МАТЕМАТИКА 196M: Дополнительные инструкции по исчислению I Семинар
Этот курс разработан как дополнение к MATH 122B. Учащиеся, зачисленные на курс, будут участвовать в еженедельном решении задач по материалу, рассмотренному в МАТЕМАТИКЕ 122B.
Учащиеся, зачисленные на курс, будут участвовать в еженедельном решении задач по материалу, рассмотренному в МАТЕМАТИКЕ 122B.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 196М-001 | Чт | 16:00–17:50 | МТЛ 123 |
МАТЕМАТИКА 196N: дополнительный учебный семинар по исчислению II
Этот курс разработан как дополнение к MATH 129.Студенты, зачисленные на курс, будут участвовать в еженедельном занятии по материалам, изучаемым в MATh229. Требуется одновременная регистрация в MATH 129.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 196N-001 | Ср | 16:00–17:50 | ЧВЭЗ 103 |
MATH 196V: семинар с дополнительными инструкциями по векторному исчислению
Этот курс разработан как дополнение к Math 223. Учащиеся, зачисленные на курс, будут участвовать в еженедельном занятии, относящемся к материалу, рассмотренному в Math 223. Требуется одновременная регистрация в Math 223.
Учащиеся, зачисленные на курс, будут участвовать в еженедельном занятии, относящемся к материалу, рассмотренному в Math 223. Требуется одновременная регистрация в Math 223.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 196V-001 | Пн | 17:30-19:20 | ПСИХИК 206 |
МАТЕМАТИКА 202: Введение в символическую логику
истинностно-функциональная логика и теория квантификации; дедуктивные методы и перевод в символическую запись.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 202-101 | Онлайн | ||
| МАТЕМАТИКА 202-201 | Онлайн |
Математика 223 Векторное исчисление (4 кредитных часа семестра) Курс охватывает дифференциальное и интегральное исчисление функций нескольких переменных. Темы включают векторные и скалярные функции, частные производные, производные по направлениям, цепное правило, локальную оптимизацию, двойные и тройные интегралы, линейный интеграл, теорему Грина, теорему Стокса и теорему о расходимости. Экзамены проходят под наблюдением.
Темы включают векторные и скалярные функции, частные производные, производные по направлениям, цепное правило, локальную оптимизацию, двойные и тройные интегралы, линейный интеграл, теорему Грина, теорему Стокса и теорему о расходимости. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 223-001 | Пн, Вт, Ср, Чт | 8:00–8:50 | ПСИХИК 205 |
| МАТЕМАТИКА 223-002 | Пн, Вт, Ср, Чт | 9:00–9:50 | ЧВЭЗ 304 |
| МАТЕМАТИКА 223-003 | Пн, Вт, Ср, Чт | 10:00–10:50 | СВЯЗЬ 311 |
| МАТЕМАТИКА 223-004 | Пн, Вт, Ср, Чт | 10:00–10:50 | ПСИХИК 307 |
| МАТЕМАТИКА 223-005 | Пн, Вт, Ср, Чт | 11:00-11:50 | ПСИХИК 307 |
| МАТЕМАТИКА 223-006 | Пн, Вт, Ср, Чт | 14:00–14:50 | ПСИХИК 307 |
| МАТЕМАТИКА 223-008 | Пн, Вт, Ср, Чт | 15:00–15:50 | ПСИХИК 205 |
| МАТЕМАТИКА 223-009 | Пн, Вт, Ср, Чт | 15:00–15:50 | ПСИХИК 204 |
| МАТЕМАТИКА 223-010 | Пн, Вт, Чт | 16:00–17:10 | ШНТЗ 247 |
| МАТЕМАТИКА 223-103 | Онлайн | ||
| МАТЕМАТИКА 223-203 | Онлайн | ||
| МАТЕМАТИКА 223-403 | Онлайн | ||
| МАТЕМАТИКА 223-503 | Онлайн |
МАТЕМАТИКА 243: Дискретная математика
теория множеств, логика, дискретные структуры; индукция и рекурсия; графы и сети; техники доказывания. Экзамены проходят под наблюдением.
Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 243-001 | Пн, Ср, Пт | 12:00-12:50 | БИОВ 219 |
| МАТЕМАТИКА 243-002 | Пн, Ср, Пт | 13:00–13:50 | ГНИЦ 222 |
| МАТЕМАТИКА 243-103 | Онлайн | ||
| МАТЕМАТИКА 243-203 | Онлайн | ||
| МАТЕМАТИКА 243-403 | Онлайн |
МАТЕМАТИКА 254: Введение в обыкновенные дифференциальные уравнения
Методы решения обыкновенных дифференциальных уравнений, качественные методы; включает подход матричных методов к решениям систем линейных уравнений и рядов. Экзамены проходят под наблюдением.
Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 254-001 | Вт, Чт | 14:00–15:15 | ПА 201 |
| МАТЕМАТИКА 254-001A | Ср | 8:00–8:50 | ЕЭК 107 |
| МАТЕМАТИКА 254-001B | Ср | 8:00–8:50 | ПА 224 |
| МАТЕМАТИКА 254-001C | Ср | 9:00–9:50 | САГХА 114 |
| МАТЕМАТИКА 254-001F | Ср | 11:00-11:50 | МЛНГ 310 |
| МАТЕМАТИКА 254-001G | Ср | 12:00-12:50 | БИОВ 208 |
| МАТЕМАТИКА 254-001H | Ср | 13:00–13:50 | ОБЕД 349 |
| МАТЕМАТИКА 254-001I | Ср | 14:00–14:50 | ГНИЦ 206 |
| МАТЕМАТИКА 254-001J | Ср | 15:00–15:50 | МЛНГ 205 |
| МАТЕМАТИКА 254-001K | Ср | 16:00–16:50 | ПСИХИЧЕСКИЙ 305 |
| МАТЕМАТИКА 254-002H | Вт, Чт | 9:30–10:45 | ГНИЦ 312 |
| МАТЕМАТИКА 254-003H | Вт, Чт | 12:30-13:45 | СВЯЗЬ 206 |
| МАТЕМАТИКА 254-103 | Онлайн | ||
| МАТЕМАТИКА 254-203 | Онлайн | ||
| МАТЕМАТИКА 254-403 | Онлайн | ||
| МАТЕМАТИКА 254-503 | Онлайн |
Организация данных; распределения, меры центра и разброса, диаграммы рассеяния, нелинейные модели и преобразования, корреляция, регрессия. Планирование экспериментов: вероятностные модели, дискретные и непрерывные случайные величины, нормальные распределения, выборочные распределения, центральная предельная теорема. Статистические выводы; доверительные интервалы и критерий значимости, t-процедуры, вывод для подсчета данных, двусторонние таблицы и процедуры хи-квадрат, вывод для регрессии, дисперсионный анализ. Экзамены проходят под наблюдением.
Планирование экспериментов: вероятностные модели, дискретные и непрерывные случайные величины, нормальные распределения, выборочные распределения, центральная предельная теорема. Статистические выводы; доверительные интервалы и критерий значимости, t-процедуры, вывод для подсчета данных, двусторонние таблицы и процедуры хи-квадрат, вывод для регрессии, дисперсионный анализ. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 263-001 | Вт, Чт | 9:30–10:45 | ЦЕСЛ 103 |
| МАТЕМАТИКА 263-001A | Пт | 8:00–8:50 | ПСИХИК 205 |
| МАТЕМАТИКА 263-001B | Пт | 9:00–9:50 | ХАРВ 313 |
| МАТЕМАТИКА 263-001C | Пт | 11:00-11:50 | ПСИХИК 207 |
| МАТЕМАТИКА 263-001D | Пт | 13:00–13:50 | ПСИХИК 207 |
| МАТЕМАТИКА 263-001E | Пт | 13:00–13:50 | ПСИХИК 206 |
| МАТЕМАТИКА 263-001F | Пт | 15:00–15:50 | ПСИХИК 204 |
| МАТЕМАТИКА 263-003HH | Пн, Ср, Пт | 8:00–8:50 | БИОВ 301 |
| МАТЕМАТИКА 263-103 | Онлайн | ||
| МАТЕМАТИКА 263-203 | Онлайн | ||
| МАТЕМАТИКА 263-403 | Онлайн |
МАТЕМАТИКА 294A: Лаборатория решения задач
Благодаря ежегодному математическому соревнованию Патнэма в качестве мотивации учащиеся еженедельно решают сложные математические задачи, решение которых требует творческого подхода, новаторского мышления и новых идей. Таким образом, эта лаборатория по решению проблем призвана помочь студентам синтезировать и применять теорию, концепции и методы, полученные в ходе их математического образования, новыми способами, которые выходят за рамки обычных учебных программ специальности.
Таким образом, эта лаборатория по решению проблем призвана помочь студентам синтезировать и применять теорию, концепции и методы, полученные в ходе их математического образования, новыми способами, которые выходят за рамки обычных учебных программ специальности.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 294A-001 | Ср | 16:00–16:50 | МТЛ 124 |
МАТЕМАТИКА 302A: Понимание элементарной математики (A)
Разработка основы для понимания общих процессов в элементарной математике, связанных с целыми числами, дробями, целыми числами и вероятностью. Этот курс предназначен только для специальностей начального образования. Экзамены проходят под наблюдением.
Этот курс предназначен только для специальностей начального образования. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 302A-001 | Пн, Ср | 14:00–15:15 | МТЛ 120 |
| МАТЕМАТИКА 302A-002 | Пн, Ср, Пт | 11:00-11:50 | МТЛ 120 |
| МАТЕМАТИКА 302A-003 | Вт, Чт | 9:30–10:45 | МТЛ 120 |
МАТЕМАТИКА 302B: Понимание элементарной математики (B)
Разработка основы для понимания общих процессов в элементарной математике, связанных с оценкой, построением графиков функций, измерением, геометрией и анализом данных. Этот курс предназначен только для специальностей начального образования. Экзамены проходят под наблюдением.
Этот курс предназначен только для специальностей начального образования. Экзамены проходят под наблюдением.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 302B-001 | Пн, Ср | 12:30-13:45 | МТЛ 120 |
| МАТЕМАТИКА 302B-002 | Вт, Чт | 11:00-12:15 | МТЛ 120 |
| МАТЕМАТИКА 302B-003 | Вт, Чт | 12:30-13:45 | МТЛ 120 |
Алгоритмический подход к решению систем линейных уравнений переходит в изучение векторов, векторных пространств и размерности. Матрицы используются для представления линейных преобразований, что приводит к собственным векторам и собственным значениям. Точное использование определений играет важную роль. Экзамены проходят под наблюдением. Этот курс необходим для изучения математики и готовит учащихся к изучению математики 323. Он является обязательным условием для большинства курсов более высокого уровня по математике.
Матрицы используются для представления линейных преобразований, что приводит к собственным векторам и собственным значениям. Точное использование определений играет важную роль. Экзамены проходят под наблюдением. Этот курс необходим для изучения математики и готовит учащихся к изучению математики 323. Он является обязательным условием для большинства курсов более высокого уровня по математике.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 313-001 | Вт, Чт | 8:00–9:15 | БИОВ 237 |
| МАТЕМАТИКА 313-002 | Пн, Ср, Пт | 10:00–10:50 | ЭНГР 304 |
| МАТЕМАТИКА 313-003 | Пн, Ср, Пт | 10:00–10:50 | САГХА 114 |
| МАТЕМАТИКА 313-004 | Вт, Чт | 12:30-13:45 | ЭДУК 310 |
| МАТЕМАТИКА 313-005 | Пн, Ср, Пт | 13:00–13:50 | ЭДУК 310 |
| МАТЕМАТИКА 313-006 | Пн, Ср, Пт | 12:00-12:50 | ПСИХИК 307 |
| МАТЕМАТИКА 313-008 | Вт, Чт | 15:30-16:45 | ПСИХИК 206 |
| МАТЕМАТИКА 313-103 | Онлайн | ||
| МАТЕМАТИКА 313-203 | Онлайн | ||
| МАТЕМАТИКА 313-403 | Онлайн | ||
| МАТЕМАТИКА 313-503 | Онлайн |
МАТЕМАТИКА 315: Введение в теорию чисел и современную алгебру
Свойства делимости целых чисел, простые числа, сравнения, квадратичные вычеты, теоретико-числовые функции.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 315-001 | Вт, Чт | 9:30–10:45 | БИОВ 237 |
МАТЕМАТИКА 322: математический анализ для инженеров
Этот курс готовит студентов к работе с линейными системами, возникающими в инженерных приложениях.Особое внимание уделяется общим принципам линейности и ортогональности. Темы включают комплексные числа и функции, матричную и векторную алгебру, линейные системы ОДУ, ряды и преобразования Фурье, разделимые уравнения в частных производных.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 322-001 | Пн, Ср, Пт | 9:00–9:50 | ХАРВ 411 |
| МАТЕМАТИКА 322-002 | Пн, Ср, Пт | 10:00–10:50 | ХАРВ 411 |
| МАТЕМАТИКА 322-003 | Вт, Чт | 9:30–10:45 | ПСИХИЧЕСКИЙ 305 |
МАТЕМАТИКА 323: формальные математические рассуждения и письмо
Элементарный реальный анализ как введение в абстрактную математику и использование математического языка.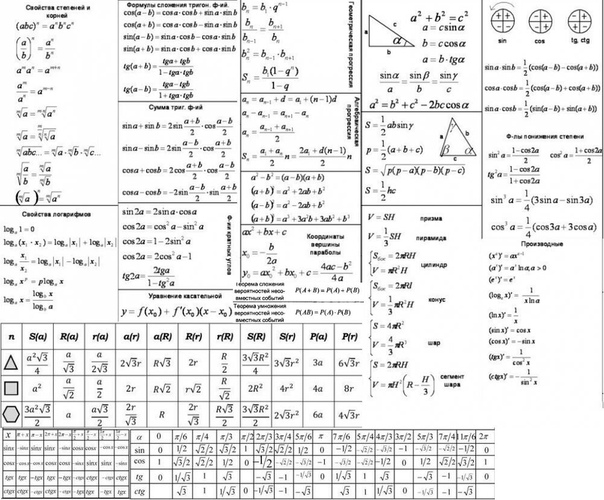 Элементарная логика и кванторы; манипуляции с множествами, отношениями и функциями, включая образы и прообразы; свойства действительных чисел; высший и инфимум; другие темы, выбранные из кардинальности, топологии реальной линии, последовательности и пределов последовательностей и функций; акцент повсюду делается на доказательстве теорем.
Элементарная логика и кванторы; манипуляции с множествами, отношениями и функциями, включая образы и прообразы; свойства действительных чисел; высший и инфимум; другие темы, выбранные из кардинальности, топологии реальной линии, последовательности и пределов последовательностей и функций; акцент повсюду делается на доказательстве теорем.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 323-001 | Пн, Ср, Пт | 10:00–10:50 | ОБЕД 331 |
| МАТЕМАТИКА 323-002 | Пн, Ср, Пт | 13:00–13:50 | БИОВ 210 |
| МАТЕМАТИКА 323-003H | Пн, Ср, Пт | 9:00–9:50 | ОБЕД 331 |
МАТЕМАТИКА 355: анализ обыкновенных дифференциальных уравнений
Линейные и нелинейные уравнения; основные методы решения; качественные и численные методы; системы уравнений; компьютерные исследования; приложения, взятые из физических, биологических и социальных наук.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 355-001 | Вт, Чт | 9:30–10:45 | ХАРВ 301 |
| МАТЕМАТИКА 355-002 | Вт, Чт | 8:00–9:15 | ПСИХИК 206 |
ДАННЫЕ 361: Элементы статистики с использованием исчисления
Сосредоточив внимание на статистических выводах, курс преследует две цели, помимо обучения статистическим методам.Один из них теоретический: исследовать связи между вероятностью, статистикой и исчислением, показывая учащимся математические основы. Применяется второй: дает опыт работы с реальными наборами данных, многие из которых имеют отношение к образованию. Учащиеся, завершившие этот курс, будут готовы преподавать курсы статистики на уровне средней школы.
Применяется второй: дает опыт работы с реальными наборами данных, многие из которых имеют отношение к образованию. Учащиеся, завершившие этот курс, будут готовы преподавать курсы статистики на уровне средней школы.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 361-001 | Пн, Ср, Пт | 13:00–13:50 | ЭДУК 240 |
МАТЕМАТИКА 361: элементы статистики с использованием исчисления
Сосредоточив внимание на статистических выводах, курс преследует две цели, помимо обучения статистическим методам.Один из них теоретический: исследовать связи между вероятностью, статистикой и исчислением, показывая учащимся математические основы. Применяется второй: дает опыт работы с реальными наборами данных, многие из которых имеют отношение к образованию. Учащиеся, завершившие этот курс, будут готовы преподавать курсы статистики на уровне средней школы.
Применяется второй: дает опыт работы с реальными наборами данных, многие из которых имеют отношение к образованию. Учащиеся, завершившие этот курс, будут готовы преподавать курсы статистики на уровне средней школы.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 361-001 | Пн, Ср, Пт | 13:00–13:50 | ЭДУК 240 |
ДАННЫЕ 363: Введение в статистические методы
Ориентированный на приложения курс статистики на основе исчисления с введением в статистическое программное обеспечение.Темы курса: Организация данных в числовом и визуальном виде. Аксиомы вероятности, условной вероятности и независимости. Случайные величины и ожидание с акцентом на параметрические семейства. Закон больших чисел и центральная предельная теорема. Оценка, систематическая ошибка и дисперсия, доверительные интервалы. Проверка гипотез, значимость и мощность. Тесты отношения правдоподобия, такие как тесты пропорций, t-тесты, тесты хи-квадрат и дисперсионный анализ.
Случайные величины и ожидание с акцентом на параметрические семейства. Закон больших чисел и центральная предельная теорема. Оценка, систематическая ошибка и дисперсия, доверительные интервалы. Проверка гипотез, значимость и мощность. Тесты отношения правдоподобия, такие как тесты пропорций, t-тесты, тесты хи-квадрат и дисперсионный анализ.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 363-001 | Вт, Чт | 9:30–10:45 | ГНИЦ 222 |
| ДАННЫЕ 363-002 | Вт, Чт | 14:00–15:15 | ПСИХИК 207 |
МАТЕМАТИКА 363: Введение в статистические методы
Ориентированный на приложения курс статистики на основе исчисления с введением в статистическое программное обеспечение. Темы курса: Организация данных в числовом и визуальном виде. Аксиомы вероятности, условной вероятности и независимости. Случайные величины и ожидание с акцентом на параметрические семейства. Закон больших чисел и центральная предельная теорема. Оценка, систематическая ошибка и дисперсия, доверительные интервалы. Проверка гипотез, значимость и мощность. Тесты отношения правдоподобия, такие как тесты пропорций, t-тесты, тесты хи-квадрат и дисперсионный анализ.
Темы курса: Организация данных в числовом и визуальном виде. Аксиомы вероятности, условной вероятности и независимости. Случайные величины и ожидание с акцентом на параметрические семейства. Закон больших чисел и центральная предельная теорема. Оценка, систематическая ошибка и дисперсия, доверительные интервалы. Проверка гипотез, значимость и мощность. Тесты отношения правдоподобия, такие как тесты пропорций, t-тесты, тесты хи-квадрат и дисперсионный анализ.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 363-001 | Вт, Чт | 9:30–10:45 | ГНИЦ 222 |
| МАТЕМАТИКА 363-002 | Вт, Чт | 14:00–15:15 | ПСИХИК 207 |
ДАННЫЕ 367: статистические методы спортивной аналитики
Этот курс познакомит вас со статистическими методами и обучением статистическому консультированию, направленному на анализ спорта с использованием данных наблюдений за игроками и командами. Уделяя особое внимание статистическим выводам и моделированию, учащиеся узнают, как анализировать проблему, связанную со спортом, использовать статистические инструменты для поиска решения и интерпретировать эти результаты спортивным профессионалам. Курс также даст возможность сосредоточиться на семестровом проекте спортивной аналитики в партнерстве с командой по легкой атлетике Университета Аризоны.
Уделяя особое внимание статистическим выводам и моделированию, учащиеся узнают, как анализировать проблему, связанную со спортом, использовать статистические инструменты для поиска решения и интерпретировать эти результаты спортивным профессионалам. Курс также даст возможность сосредоточиться на семестровом проекте спортивной аналитики в партнерстве с командой по легкой атлетике Университета Аризоны.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 367-001 | Пн, Ср | 15:00–16:15 | ПСИХИК 207 |
ДАННЫЕ 375: Введение в статистические вычисления
Базовые вычислительные навыки, включая генерацию случайных величин, интеграцию методом Монте-Карло, визуализацию, методы оптимизации, методы повторной выборки, байесовские подходы и введение в среды статистических вычислений (R и Python). Материал предоставит практический опыт решения реальных проблем. Ожидается, что у студентов есть опыт работы с языком программирования, предпочтительно с Python.
Материал предоставит практический опыт решения реальных проблем. Ожидается, что у студентов есть опыт работы с языком программирования, предпочтительно с Python.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 375-001 | Вт, Чт | 8:00–9:15 | ШНТЗ 247 |
МАТЕМАТИКА 391: Наставничество
Специализированная работа на индивидуальной основе, состоящая из инструктажа и практики в реальном служении отделу, программе или дисциплине.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 391-203 | Онлайн |
МАТЕМАТИКА 396L: Семинар по доказательствам диких кошек
Этот курс разработан как дополнение к Math 323.![]() Учащиеся, зачисленные на курс, будут участвовать в еженедельных задачах, относящихся к материалу, изложенному в Math 323. Основная цель этого курса — предоставить учащимся много возможностей поделиться своими математическими предположениями и их обоснованиями с одноклассниками. Во время занятий студенты будут обсуждать правильность математических утверждений и формальных доказательств. Требуется одновременная регистрация в Math 323.
Учащиеся, зачисленные на курс, будут участвовать в еженедельных задачах, относящихся к материалу, изложенному в Math 323. Основная цель этого курса — предоставить учащимся много возможностей поделиться своими математическими предположениями и их обоснованиями с одноклассниками. Во время занятий студенты будут обсуждать правильность математических утверждений и формальных доказательств. Требуется одновременная регистрация в Math 323.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 396L-001 | Ср | 15:00–16:50 | ГНИЦ 222 |
МАТЕМАТИКА 401B: символьная логика
Продвинутая логика высказываний и теория квантификации; метатеоремы о непротиворечивости, независимости и полноте; теория множеств, теория чисел и модальная теория; теория рекурсивных функций и теорема Геделя о неполноте.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 401B-002 | Вт, Чт | 11:00-12:15 | Онлайн |
МАТЕМАТИКА 406A: Учебная программа и оценивание по математике в средней школе
Изучение учебных программ по математике для средней школы с упором на разработку математических тем; изучение оценивания с упором на его согласование с инструкцией; и практический опыт с упором на анализ учебной программы и реализацию мер оценки.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 406A-001 | Вт, Чт | 14:00–15:15 | МТЛ 120 |
МАТЕМАТИКА 413: линейная алгебра
Векторные пространства, линейные преобразования и матрицы, определители, собственные значения и диагонализация, билинейные формы, ортогональные и унитарные преобразования, каноническая форма Жордана.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 413-001 | Пн, Ср, Пт | 13:00–13:50 | МЛНГ 303 |
МАТЕМАТИКА 415B: второй курс абстрактной алгебры
Продолжение MATH 415A/515A.Темы могут включать конечные группы, матричные группы, теорию Галуа, линейную и полилинейную алгебру, конечные поля и теорию кодирования.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 415B-001 | Пн, Ср, Пт | 11:00-11:50 | МТЛ 124 |
МАТЕМАТИКА 422: Высшая прикладная математика
Приложения векторного исчисления, комплексных переменных и теории Штурма-Лиувилля. Ряды Фурье, преобразования Фурье и Лапласа и разделение переменных в классических уравнениях в частных производных. Этот курс использует более математический подход, чем Math 322.
Ряды Фурье, преобразования Фурье и Лапласа и разделение переменных в классических уравнениях в частных производных. Этот курс использует более математический подход, чем Math 322.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 422-001 | Вт, Чт | 12:30-13:45 | ЭДУК 240 |
МАТЕМАТИКА 424: теория комплексных переменных
Комплексные числа, аналитические функции, гармонические функции, элементарные функции, комплексное интегрирование, интегральная теорема Коши, представление рядов аналитических функций, теория вычетов, конформное отображение, приложения.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 424-001 | Вт, Чт | 14:00–15:15 | ШНТЗ 247 |
МАТЕМАТИКА 425B: реальный анализ нескольких переменных
Непрерывность и дифференциация в высших измерениях, кривых и поверхностях; изменение координат; теоремы Грина, Гаусса и Стокса; теоремы об обратной и неявной функциях.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 425B-001 | Пн, Ср, Пт | 10:00–10:50 | БИОВ 219 |
МАТЕМАТИКА 432: топологические пространства
Теория множеств (счетность/несчетность), топологические пространства и непрерывные отображения, метрические пространства, связность и компактность, аксиомы отделимости и хаусдорфовы пространства, теорема Тихонова о произведении, вводные темы из алгебраической топологии (гомотопия, фундаментальная группа) или теории категорий.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 432-001 | Пн, Ср, Пт | 9:00–9:50 | ПСИХИК 207 |
МАТЕМАТИКА 445: Введение в криптографию
[Ведёт весенний семестр в четные годы].Введение в криптосистемы и криптоанализ. Основная теория чисел и конечные поля. Базовая теория сложности и вероятности. Протоколы RSA и Диффи-Хеллмана, факторизация и атаки на дискретные журналы. Расширенный стандарт шифрования. Дополнительные темы как раз позволяет.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 445-001 | Пн, Ср, Пт | 14:00–14:50 | ЭДУК 240 |
МАТЕМАТИКА 454: обыкновенные дифференциальные уравнения и теория устойчивости
Общая теория начальных задач, линейные системы и фазовые портреты, линеаризация нелинейных систем, теория устойчивости и бифуркаций, введение в хаотическую динамику.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 454-001 | Пн, Ср, Пт | 14:00–14:50 | ПСИХИК 207 |
МАТЕМАТИКА 456: прикладные дифференциальные уравнения в частных производных
Свойства уравнений в частных производных и методы их решения: методы Фурье, функции Грина, численные методы.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 456-001 | Пн, Ср, Пт | 11:00-11:50 | ЭНГР 304 |
| МАТЕМАТИКА 456-002 | Пн, Ср, Пт | 13:00–13:50 | БИОВ 237 |
ДАННЫЕ 462: Финансовая математика
Анализ денежных потоков с актуарной точки зрения. Теория процентов, аннуитеты, облигации, ссуды и связанные с ними портфели с фиксированным доходом, норма прибыли, доходность, продолжительность, иммунизация и связанные с ними концепции.
Теория процентов, аннуитеты, облигации, ссуды и связанные с ними портфели с фиксированным доходом, норма прибыли, доходность, продолжительность, иммунизация и связанные с ними концепции.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 462-001 | Пн, Ср, Пт | 9:00–9:50 | ГНИЦ 411 |
МАТЕМАТИКА 462: Финансовая математика
Анализ денежных потоков с актуарной точки зрения.Теория процентов, аннуитеты, облигации, ссуды и связанные с ними портфели с фиксированным доходом, норма прибыли, доходность, продолжительность, иммунизация и связанные с ними концепции.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 462-001 | Пн, Ср, Пт | 9:00–9:50 | ГНИЦ 411 |
МАТЕМАТИКА 464: теория вероятностей
Пространства вероятностей, случайные величины, слабый закон больших чисел, центральная предельная теорема, различные дискретные и непрерывные распределения вероятностей.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 464-001 | Вт, Чт | 9:30–10:45 | ЧВЭЗ 303 |
| МАТЕМАТИКА 464-002 | Пн, Ср, Пт | 9:00–9:50 | АНГР 311 |
МАТЕМАТИКА 466: теория статистики
Теория выборки.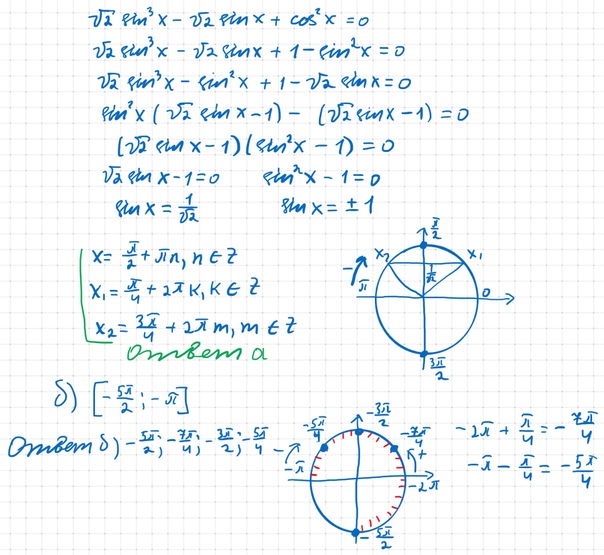 Балльная оценка. Ограничение раздачи. Проверка гипотез. Доверительные интервалы. Методы больших выборок.
Балльная оценка. Ограничение раздачи. Проверка гипотез. Доверительные интервалы. Методы больших выборок.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 466-001 | Вт, Чт | 9:30–10:45 | ХАРВ 319 |
| МАТЕМАТИКА 466-002 | Вт, Чт | 14:00–15:15 | ЭДУК 240 |
| МАТЕМАТИКА 466-003 | Вт, Чт | 9:30–10:45 | ВЫКЛ. В РЕЖИМЕ ОНЛАЙН |
ДАННЫЕ 467: Введение в прикладную регрессию и обобщенные линейные модели
Прикладной курс линейной регрессии, дисперсионного анализа и обобщенных линейных моделей для студентов, прошедших курс основных статистических методов. Акцент делается на практических методах анализа данных и их интерпретации с использованием статистического программного обеспечения, такого как R. Содержание курса включает построение моделей; линейная регрессия; регрессионная и остаточная диагностика; основные экспериментальные планы, такие как однофакторный и двухфакторный дисперсионный анализ; блочные конструкции и модели со случайными эффектами; введение в экспоненциальные семейства и обобщенные линейные модели, включая логистическую регрессию и регрессию Пуассона. Некоторый акцент будет сделан на матричных представлениях и эффективных вычислительных методах.
Акцент делается на практических методах анализа данных и их интерпретации с использованием статистического программного обеспечения, такого как R. Содержание курса включает построение моделей; линейная регрессия; регрессионная и остаточная диагностика; основные экспериментальные планы, такие как однофакторный и двухфакторный дисперсионный анализ; блочные конструкции и модели со случайными эффектами; введение в экспоненциальные семейства и обобщенные линейные модели, включая логистическую регрессию и регрессию Пуассона. Некоторый акцент будет сделан на матричных представлениях и эффективных вычислительных методах.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 467-103 | Онлайн |
ДАННЫЕ 468: прикладные стохастические процессы
Приложения гауссовских и марковских процессов и теории восстановления; Винеровские и пуассоновские процессы, очереди.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 468-001 | Вт, Чт | 14:00–15:15 | БИОВ 237 |
МАТЕМАТИКА 468: прикладные стохастические процессы
Приложения гауссовских и марковских процессов и теории восстановления; Винеровские и пуассоновские процессы, очереди.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 468-001 | Вт, Чт | 14:00–15:15 | БИОВ 237 |
МАТЕМАТИКА 485: математическое моделирование
Разработка, анализ и оценка математических моделей для физических, биологических, социальных и технических проблем; требуются как аналитические, так и численные методы решения.
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| МАТЕМАТИКА 485-103 | Онлайн | ||
| МАТЕМАТИКА 485-203 | Онлайн | ||
| МАТЕМАТИКА 485-403 | Онлайн |
ДАННЫЕ 498A: Краеугольный камень для статистики и науки о данных
Завершающий опыт, который знакомит студентов с разработкой, анализом, оценкой и передачей статистического и научного анализа данных для физических, биологических, социальных и других проблем анализа данных.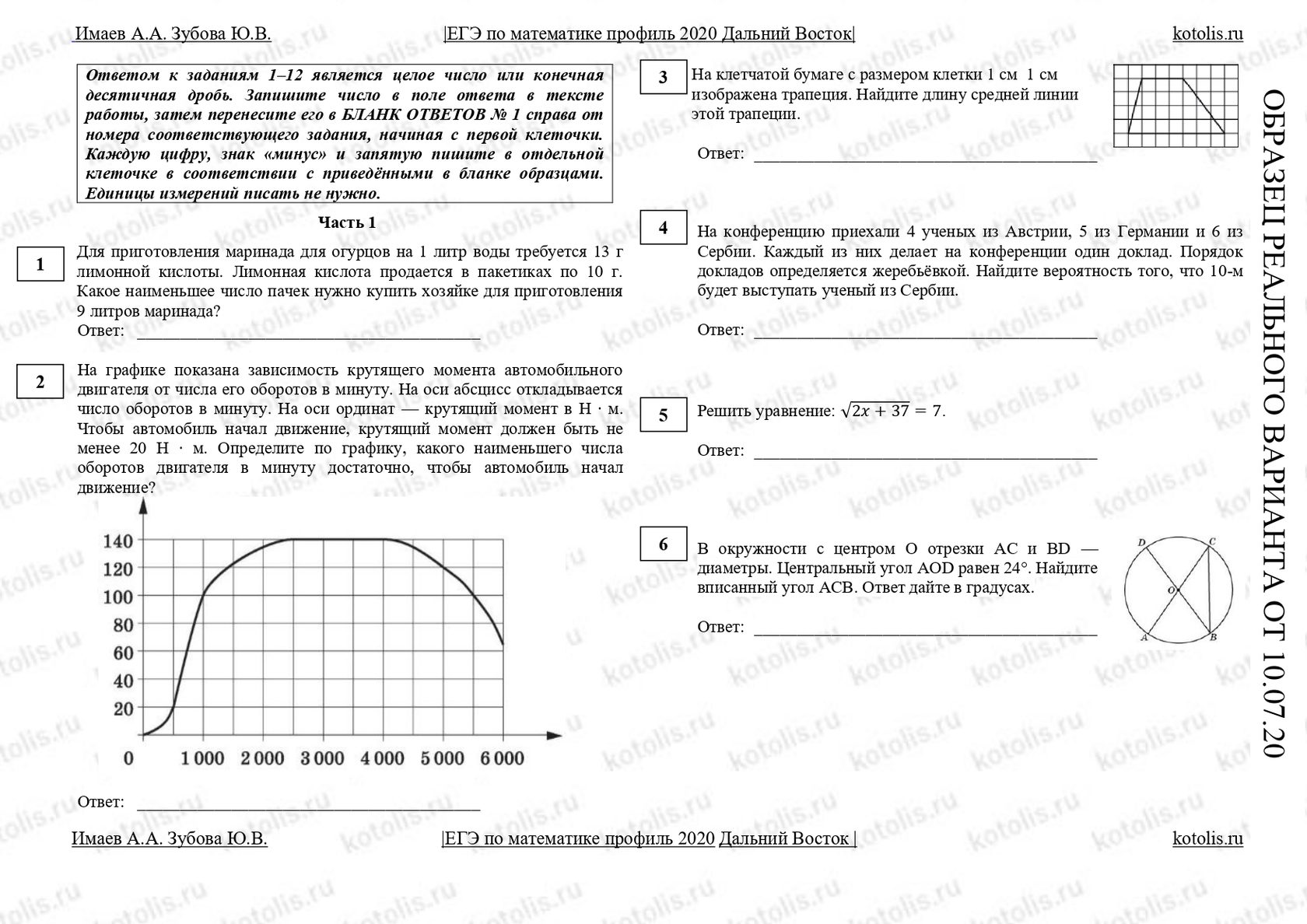
Просмотр информации о разделе
| Раздел | дней | Время | Местоположение |
|---|---|---|---|
| ДАННЫЕ 498A-001 | Вт, Чт | 11:00-12:15 | БИОВ 219 |
Профилирование математических процедурных навыков и навыков решения задач у студентов бакалавриата по новой учебной программе по математике
1.Введение
На международном уровне стремление иметь счетных граждан желательно из-за его преимуществ для экономики страны в целом (Gal and UNESCO, 2020; IBEC, 2015). Это желание ничем не отличается от Ирландии (DES, 2010; SOLAS, 2020). Эти стремления обусловлены необходимостью оставаться конкурентоспособными с европейской и международной точки зрения (Mullis et al. , 2020; Perkins & Clerkin, 2020), а также исторически продемонстрированной низкой успеваемостью ирландских студентов по сравнению с международными (Humphreys, 2015).Поэтому всегда приветствуются исследования, которые обеспечивают платформу для новых идей, которые могут способствовать улучшению навыков счета. Это исследование направлено на использование диагностического тестирования для изучения и сравнения процедурных математических навыков и навыков решения задач у начинающих студентов бакалавриата в Ирландии.
, 2020; Perkins & Clerkin, 2020), а также исторически продемонстрированной низкой успеваемостью ирландских студентов по сравнению с международными (Humphreys, 2015).Поэтому всегда приветствуются исследования, которые обеспечивают платформу для новых идей, которые могут способствовать улучшению навыков счета. Это исследование направлено на использование диагностического тестирования для изучения и сравнения процедурных математических навыков и навыков решения задач у начинающих студентов бакалавриата в Ирландии.
1.1. Контекст с точки зрения Ирландии
За последнее десятилетие Ирландия выдвинула несколько инициатив, чтобы попытаться поддержать и улучшить преподавание и изучение математики на всех уровнях образовательного сектора.Одной из таких крупных инициатив было введение в 2010 г. учебной программы по математике на втором уровне образования, которая должна была изменить акцент преподавания и обучения с традиционного заучивания «мелом и разговорами» (Hourigan & O’Donoghue, 2007) на более ориентированное на учащихся подход, в котором основное внимание уделялось реальному пониманию, решению проблем и применению математических навыков в незнакомых контекстах (DES, 2010).
В связи с введением другой учебной программы по математике на втором уровне образования в Ирландии 10 лет назад была разработана и реализована еще одна важная инициатива под названием «Профессиональный диплом по математике для преподавания».Это полноценная программа уровня 8, целью которой является повышение квалификации внештатных учителей математики в ирландских школах второго уровня. Отчет, проведенный Ни Риордейн и Ханниган в 2009 году, показал, что почти 50% учителей, преподающих математику в школах второго уровня в Ирландии, не имеют для этого квалификации, то есть они имеют квалификацию в предметных дисциплинах, отличных от математики, однако они были назначены преподавать математику в классах. в своих школах (Ríordain & Hannigan, 2011). Этих учителей называют учителями математики «вне поля», и было сочтено, что для успешного внедрения ПМ в школах второго уровня в Ирландии для этого необходимы учителя с соответствующей квалификацией (Goos et al., 2020). Правительство Ирландии финансировало эту программу, чтобы все внештатные учителя, желающие участвовать, могли сделать это бесплатно для себя, за исключением того, что в большинстве случаев они тратят много времени на преподавание на полную ставку.
Кроме того, правительство Ирландии заказало обзор структуры начального педагогического образования (ITE) в Ирландии, который был проведен Паси Сальбергом, международным экспертом из Финляндии, и результаты были изложены в так называемом «Отчете Сальберга». ‘ в 2012.В этом отчете содержится много рекомендаций, включая изменение программ ITE, чтобы они стали магистерскими программами уровня 9 Quality and Qualifications Ireland (QQI) там, где они были уровнем QQI 8 до этого обзора (см. Раздел ниже для объяснения наград QQI). Это еще раз подчеркнуло важность и внимание, уделяемое улучшению математического образования и ирландской системы образования в целом.
Этот значительный период изменений в ирландской системе образования в целом (Sahlberg, 2012) и в системе математического образования в частности (DES, 2010; Goos et al., 2020), предполагалось, что это приведет к улучшению успеваемости студентов-математиков второго уровня и, в свою очередь, студентов-математиков высших учебных заведений. Таким образом, исследование, изложенное в этой статье, имеет огромное значение, поскольку оно направлено на непосредственное изучение того, привели ли время и инвестиции в пересмотр учебной программы по математике второго уровня к ощутимым улучшениям в математических способностях учащихся, как это было задумано. Это не было исследовано и сообщено до настоящего времени. Некоторые из предварительных исследований, связанных с математикой проекта (Prendergast et al., 2017; Treacy & Faulkner, 2015), а также литература, относящаяся конкретно к этому исследованию, а именно в области процедурных навыков и навыков решения задач в математике, будут изложены в последующем обзоре литературы.
Таким образом, исследование, изложенное в этой статье, имеет огромное значение, поскольку оно направлено на непосредственное изучение того, привели ли время и инвестиции в пересмотр учебной программы по математике второго уровня к ощутимым улучшениям в математических способностях учащихся, как это было задумано. Это не было исследовано и сообщено до настоящего времени. Некоторые из предварительных исследований, связанных с математикой проекта (Prendergast et al., 2017; Treacy & Faulkner, 2015), а также литература, относящаяся конкретно к этому исследованию, а именно в области процедурных навыков и навыков решения задач в математике, будут изложены в последующем обзоре литературы.
1.2. Объяснение наград организации Quality and Qualifications Ireland (QQI)
Награды QQI — это награды, установленные организацией Quality and Qualifications Ireland, в которых описывается спектр наград второго уровня и высшего образования, начиная от уровня QQI 1 (сертификат) до уровня QQI 10 (докторская степень). награды).Если учащиеся успешно заканчивают образование второго уровня в Ирландии, они достигают уровня 5, а высшее образование предлагает программы/сертификаты/курсы от уровня 6 до уровня 10. Эта национальная структура для наград второго уровня и более высокого уровня в Ирландии позволяет проводить сравнение, прозрачность и признание наград. на разных уровнях. Это также позволяет людям создавать свои собственные персонализированные точки входа и выхода через систему образования в зависимости от их опыта, целей и возможностей.
награды).Если учащиеся успешно заканчивают образование второго уровня в Ирландии, они достигают уровня 5, а высшее образование предлагает программы/сертификаты/курсы от уровня 6 до уровня 10. Эта национальная структура для наград второго уровня и более высокого уровня в Ирландии позволяет проводить сравнение, прозрачность и признание наград. на разных уровнях. Это также позволяет людям создавать свои собственные персонализированные точки входа и выхода через систему образования в зависимости от их опыта, целей и возможностей.
2.Обзор литературы
2.1. Предварительное исследование математических способностей учащихся после введения Project Maths
Трейси и Фолкнер (2015) провели одно из первых исследований, чтобы выяснить, произошли ли какие-либо изменения в математических способностях учащихся после введения PM. Их исследование изучало основные математические навыки студентов при поступлении в бакалавриат и основывалось на работе Gill et al. (2010) и Faulkner et al. (2014, 2020), все из которых сообщили о неуклонном снижении базовых математических навыков учащихся с течением времени.Хотя Трейси и Фолкнер (2015) также обнаружили, что снижение базовых математических навыков студентов при поступлении в высшие учебные заведения продолжилось после введения PM, они указали на то, что навыки решения задач у студентов улучшились за этот период изменений. Однако исследование пришло к выводу, что необходимы более тщательные исследования в этой области.
(2014, 2020), все из которых сообщили о неуклонном снижении базовых математических навыков учащихся с течением времени.Хотя Трейси и Фолкнер (2015) также обнаружили, что снижение базовых математических навыков студентов при поступлении в высшие учебные заведения продолжилось после введения PM, они указали на то, что навыки решения задач у студентов улучшились за этот период изменений. Однако исследование пришло к выводу, что необходимы более тщательные исследования в этой области.
В дополнение к этому Prendergast et al. (2017) исследовали навыки решения проблем у студентов после введения Project Math с точки зрения преподавателей и обнаружили, что преподаватели считают, что их студенты были, по крайней мере, более открытыми и готовыми участвовать в решении проблем, чем они были в когортах, которые продолжали PM.И снова эта работа потребовала проведения дальнейших исследований для получения более точных результатов.
В дополнение к этим двум исследованиям, пилотное исследование для исследования, о котором будет сообщено в этой статье, использовало новый диагностический тест, разработанный авторами (методология которого будет изложена позже в документе), чтобы дополнительно изучить, есть ли у студентов проблемы. навыки решения улучшились после введения PM. Исследование, в котором сравнивались навыки решения задач и процедурные навыки студентов по математике, показало, что процедурные навыки студентов были статистически значимо лучше, чем их навыки решения задач (Faulkner et al., 2020). Это исследование имело относительно небольшой размер выборки (95 168 n 95 169 = 87) и изучало только студентов инженерных специальностей и учебных заведений. Таким образом, настоящее исследование направлено на то, чтобы изложить результаты более обширной работы, проведенной в течение более длительного периода времени, с большим размером выборки и большим количеством областей дисциплины, чтобы определить, можно ли сделать более убедительные выводы о математических способностях учащихся с точки зрения решения задач и процедурные навыки пост ПМ. Прежде чем наметить эту работу, важно рассмотреть литературу, касающуюся решения проблем и процедурных навыков, чтобы было ясно, что означает каждый термин в данном случае этого исследования.
навыки решения улучшились после введения PM. Исследование, в котором сравнивались навыки решения задач и процедурные навыки студентов по математике, показало, что процедурные навыки студентов были статистически значимо лучше, чем их навыки решения задач (Faulkner et al., 2020). Это исследование имело относительно небольшой размер выборки (95 168 n 95 169 = 87) и изучало только студентов инженерных специальностей и учебных заведений. Таким образом, настоящее исследование направлено на то, чтобы изложить результаты более обширной работы, проведенной в течение более длительного периода времени, с большим размером выборки и большим количеством областей дисциплины, чтобы определить, можно ли сделать более убедительные выводы о математических способностях учащихся с точки зрения решения задач и процедурные навыки пост ПМ. Прежде чем наметить эту работу, важно рассмотреть литературу, касающуюся решения проблем и процедурных навыков, чтобы было ясно, что означает каждый термин в данном случае этого исследования.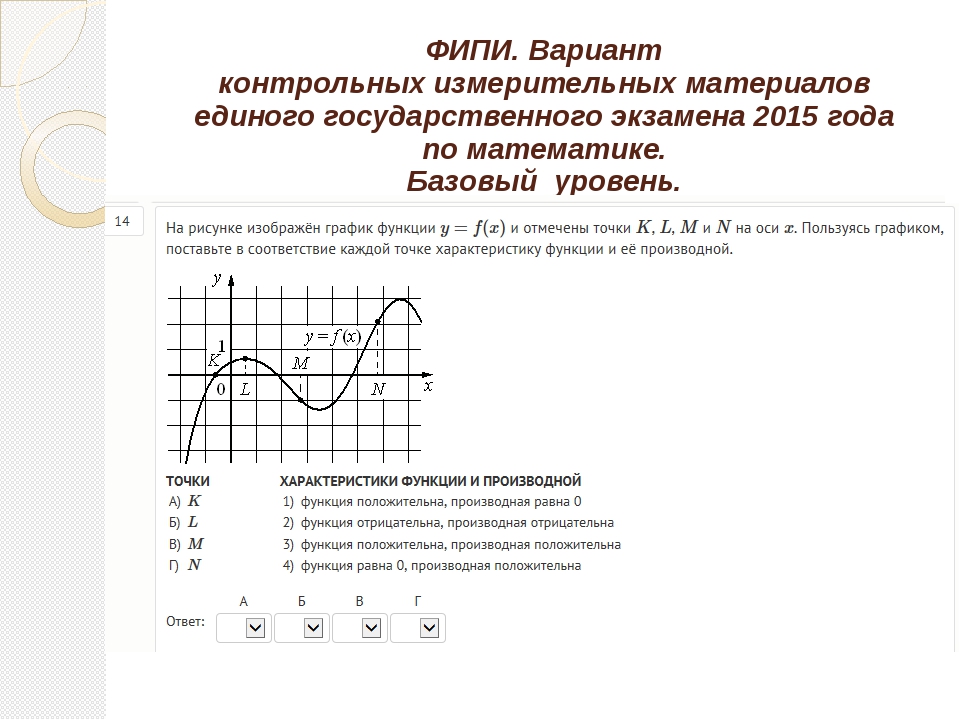
2.2. Mathematical proficiency
Значение того, что считается успешным преподаванием и изучением математики, изменилось на международном уровне за последние несколько десятилетий в ответ на социальные и образовательные изменения (Kilpatrick et al., 2001). Поэтому трудно использовать один термин, с которым согласны все заинтересованные стороны в математическом образовании, чтобы охватить все аспекты опыта, компетентности, знаний и способностей в области математики. Однако Mathematical Proficiency стал общепринятым термином для обозначения такого набора навыков.Он используется в контексте ирландской учебной программы по математике, как и многие другие, и считается, что он состоит из следующих пяти компонентов:
концептуальное понимание – понимание математических понятий, операций и отношений
беглость процедур – умение выполнять процедуры гибко, точно, эффективно и надлежащим образом
стратегическая компетентность – способность формулировать, представлять и решать математические задачи
адаптивное мышление – способность к логическому мышлению, размышлению, объяснению и обоснованию
продуктивная предрасположенность – привычная склонность считать математику разумной, полезной и полезной в сочетании с верой в прилежание и собственную эффективность.
 (DES, 2017, стр. 5)
(DES, 2017, стр. 5)
Важно отметить, что пять направлений переплетаются и взаимозависимы в развитии математических навыков (Kilpatrick et al., 2001). Следующие разделы этого обзора литературы сосредоточены исключительно на первых двух компонентах, перечисленных выше, поскольку они находятся в центре внимания диагностического теста, содержащегося в этом исследовании. Однако все компоненты переплетены, если мы хотим добиться успеха в достижении математических знаний.
2.3. Процедурные навыки в математике
Процедурные навыки в математике были определены как критический компонент в обучении математике (NCTM, 2014a). В литературе они определяются по-разному, например, как последовательность действий для решения проблем (Rittle-Johnson & Alibali, 1999). Другие описывают владение процедурными навыками как способность знать, как что-то происходит определенным образом (Hiebert & Leferve, 1986). С другой стороны, некоторые альтернативные определения придают набору навыков меньшее значение. Например, Арслан (2010) описал процедурное мастерство как обучение, которое включает исключительно запоминание операций без понимания лежащих в их основе значений. Однако противоречивые мнения относительно этого последнего определения утверждают, что способность успешно выполнять процедурные навыки в математике и, следовательно, развивать процедурную беглость — это гораздо больше, чем просто запоминание фактов и процедур или знание того, когда использовать одну процедуру вместо другой в данной ситуации, а скорее то, что процедурная беглость основывается на концептуальном понимании, стратегическом мышлении и решении проблем (NCTM, 2000, 2014a, 2014b; NGA Center & CCSSO, 2010).
Например, Арслан (2010) описал процедурное мастерство как обучение, которое включает исключительно запоминание операций без понимания лежащих в их основе значений. Однако противоречивые мнения относительно этого последнего определения утверждают, что способность успешно выполнять процедурные навыки в математике и, следовательно, развивать процедурную беглость — это гораздо больше, чем просто запоминание фактов и процедур или знание того, когда использовать одну процедуру вместо другой в данной ситуации, а скорее то, что процедурная беглость основывается на концептуальном понимании, стратегическом мышлении и решении проблем (NCTM, 2000, 2014a, 2014b; NGA Center & CCSSO, 2010).
2.4. Проблемы, связанные с навыками решения задач по математике
Литература, посвященная решению задач по математике, состоит из больших вариаций того, что исследователи/системы образования/экономика определяют как решение задач (Kilpatrick, 1969). Несмотря на часто противоречащие друг другу определения, остается одна константа, которая заключается в признании и поддержке педагогами и экономистами необходимости иметь студентов и граждан, которые могут быть гибкими и успешно решать проблемы в математике (IBEC, 2015). Поэтому этот желаемый набор навыков востребован многими работодателями и высшими учебными заведениями (CBI, 2006; Mills & Treagust, 2003; NCETM, 2009; Vorderman et al., 2011; Walport et al., 2010).
Поэтому этот желаемый набор навыков востребован многими работодателями и высшими учебными заведениями (CBI, 2006; Mills & Treagust, 2003; NCETM, 2009; Vorderman et al., 2011; Walport et al., 2010).
Перкинс (1993) обсуждает желание обучать студентов математике так, чтобы они фундаментально понимали математику, которой они занимаются, и, в свою очередь, могли продемонстрировать такую гибкость применения своих навыков к различным проблемам, с которыми они сталкиваются. Это стремление научить навыкам решения задач отражено в большей части литературы по математическому образованию (Foshay & Kirkley, 2003; Jozwiak, 2004; Reif, 1981).К сожалению, именно этот желаемый набор навыков эффективного решения проблем, как часто сообщается, отсутствует у выпускников школ (ACT, 2006; Jones et al., 2015; Toner, 2011). Однако это не проблема, о которой недавно сообщалось. Проблемы, с которыми сталкиваются многие учащиеся, пытаясь применить математику, которой они занимались в условиях формального образования, в условиях рабочего места или даже в интересах дальнейшего изучения формальной математики, описаны в литературе в течение длительного времени.![]() длительное время (Фолкнер и др., 2020; Хаттон, 1998 г.; Трейлибс, 1979).
длительное время (Фолкнер и др., 2020; Хаттон, 1998 г.; Трейлибс, 1979).
Таким образом, все заинтересованные стороны в обществе согласны с тем, что эффективные навыки решения математических задач чрезвычайно желательны для учащихся по многим причинам и что в настоящее время они часто не распространены среди большинства выпускников школ. Именно такие выводы привели к тому, что некоторые страны пытаются адаптировать свои системы образования к системам, в которых преподавание и обучение навыкам решения проблем могут использоваться более успешно, чем в настоящее время (OECD, 2009a, 2009b; QCA, 2008; Soh, 2008).Однако никогда не недооценивалась задача улучшения преподавания и обучения в области навыков решения проблем (Wallace et al., 2009). В следующих разделах будет обсуждаться некоторая литература в области определения общего решения задач и решения задач в математике, а также особенности этого в ирландском контексте, чтобы пролить свет на это исследование и то, как была выбрана методология.
2.5. Общие навыки решения проблем и навыки решения конкретных дисциплин
Процесс применения метода, который не обязательно был ранее известен или полностью понят, к неизвестной проблеме, которая имеет определенные условия, является сущностью настоящего решения проблем.Чтобы добиться успеха в решении общих проблем, вы должны быть способны к критическому мышлению (анализу, исследованиям и общению) и эффективному принятию решений (Hayes, 1989). Модели для решения общих проблем часто предлагаются в контексте обучения, чтобы помочь преподавателям и учащимся научиться решать проблемы. Одна такая модель была предложена Woods et al. (1975) и включает в себя использование следующих шагов: определить проблему, подумать о проблеме, спланировать решение, выполнить план и оглянуться назад.
Ценные атрибуты общего решения задач, а также примерная модель того, как его выполнять, могут и применялись для решения задач конкретно в математике (Blum & Niss, 1991) и даже в других областях дисциплины (Wang 2019) . Чтобы добиться успеха в решении проблем, особенно в математике, требуется способность использовать и применять математические концепции, а также понимать связи между областями содержания и эффективно понимать, как математика в том виде, в каком мы ее знаем, возникла и развивалась (Shiel & Kelleher, 2017).Начальное педагогическое образование теперь признает это и поэтому фокусируется не только на общей педагогике в передовой образовательной практике, но и на педагогике, специфичной для математики (O’Meara & Faulkner, 2021). Далее рассматривается решение математических задач, специфичных для контекста этого исследования, с целью понять, как решение об оценке этих навыков таким образом, как они оцениваются, было принято в рамках этого исследования.
Чтобы добиться успеха в решении проблем, особенно в математике, требуется способность использовать и применять математические концепции, а также понимать связи между областями содержания и эффективно понимать, как математика в том виде, в каком мы ее знаем, возникла и развивалась (Shiel & Kelleher, 2017).Начальное педагогическое образование теперь признает это и поэтому фокусируется не только на общей педагогике в передовой образовательной практике, но и на педагогике, специфичной для математики (O’Meara & Faulkner, 2021). Далее рассматривается решение математических задач, специфичных для контекста этого исследования, с целью понять, как решение об оценке этих навыков таким образом, как они оцениваются, было принято в рамках этого исследования.
2.6. Проект Математика и навыки решения задач
Как упоминалось ранее, в зависимости от контекста и культуры, в рамках которой обсуждается решение задач по математике, «задача» может быть определена по-разному и решаться с использованием разных методов (Schoenfeld, 2016) . Имея это в виду, McClure (2013) выделяет два конца спектра решения проблем, чтобы продемонстрировать различные определения.
Имея это в виду, McClure (2013) выделяет два конца спектра решения проблем, чтобы продемонстрировать различные определения.
То, что МакКлюр (2013) описывает как менее экстремальный конец шкалы решения проблем, — это тот, в котором основное внимание уделяется использованию предписанной техники, которая ранее наблюдалась и использовалась для решения набора «проблем». В контексте класса это может проявляться в том, что учащиеся используют метод решения проблем, который учитель изложил и продемонстрировал на нескольких разных примерах.Проблемы, связанные с этой техникой, часто схожи и предсказуемы для развития определенного навыка. На другом конце спектра решения проблем, который МакКлюр (2013) считает более экстремальным, человек занимается тем, что считается более реалистичными проблемами: угадыванием, открытием и осмыслением математики. Эту идею решения проблем можно сравнить с интерпретацией Полиа (Polya, 1945), согласно которой реальные проблемы не обязательно должны быть приложениями «реального мира», но могут быть проблемами, содержащимися в самой математике. В первую очередь нестандартный и непривычный характер таких задач отличает их от первого типа обсуждаемого решения проблем. Таким образом, решение проблем на более экстремальном конце спектра МакКлюра, как правило, связано со следующим:
В первую очередь нестандартный и непривычный характер таких задач отличает их от первого типа обсуждаемого решения проблем. Таким образом, решение проблем на более экстремальном конце спектра МакКлюра, как правило, связано со следующим:
Сосредоточенность на поиске решения, а не на запоминании процедур
Сосредоточенность на изучении паттернов, а не на запоминании процедур
Акцент на формулировании предположений, а не просто на практических вопросах.
В то время как многие другие исследователи давали другие интерпретации решения проблем, большинство из них попадают в спектр двух крайностей, обсуждаемых здесь (Foshay & Kirkley, 2003). В следующем разделе будет обсуждаться это определение решения проблем в контексте учебной программы PM в Ирландии.
2.7. Ирландское математическое образование второго уровня и решение задач
При изучении программы PM можно увидеть, что решение задач соответствует нескольким интерпретациям с точки зрения того, как оно определяется и как программа предназначена для его реализации. Учителя и ученики должны рассматривать решение проблем в соответствии с моделью, описанной Пойей (1945). До введения PM учебная программа уделяла особое внимание решению проблем, которое было направлено на решение набора ранее встречавшихся проблем (или их версий) с использованием предписанной техники, т. е. той, которая описана МакКлюром (2013) для неэкстремальных конец ее спектра решения проблем. Тем не менее, учебная программа Project Maths требует, чтобы решение задач в ирландских классах было отодвинуто на другой конец спектра МакКлюра и больше соответствовало модели Пойи.Как показано в этой модели, учащиеся должны участвовать в реальном решении незнакомых задач посредством догадок, открытий и осмысления математики. Об этом свидетельствует описание решения проблем в программе PM:
Учителя и ученики должны рассматривать решение проблем в соответствии с моделью, описанной Пойей (1945). До введения PM учебная программа уделяла особое внимание решению проблем, которое было направлено на решение набора ранее встречавшихся проблем (или их версий) с использованием предписанной техники, т. е. той, которая описана МакКлюром (2013) для неэкстремальных конец ее спектра решения проблем. Тем не менее, учебная программа Project Maths требует, чтобы решение задач в ирландских классах было отодвинуто на другой конец спектра МакКлюра и больше соответствовало модели Пойи.Как показано в этой модели, учащиеся должны участвовать в реальном решении незнакомых задач посредством догадок, открытий и осмысления математики. Об этом свидетельствует описание решения проблем в программе PM:
Решение проблем означает участие в задаче, решение которой не очевидно сразу. Решение задач является неотъемлемой частью математического обучения. В повседневной жизни и на рабочем месте способность решать проблемы является очень полезным навыком. На уроках математики решение задач не должно встречаться изолированно, а должно проникать во все аспекты преподавания и обучения.Проблемы могут касаться чисто математических вопросов или некоторого прикладного контекста. (DES, 2011, стр. 10)
На уроках математики решение задач не должно встречаться изолированно, а должно проникать во все аспекты преподавания и обучения.Проблемы могут касаться чисто математических вопросов или некоторого прикладного контекста. (DES, 2011, стр. 10)
Учебная программа PM и ее акцент с точки зрения решения проблем теперь также можно рассматривать в большей степени в соответствии с техническим отчетом Программы оценки иностранных студентов (PISA) (2012), в котором особое внимание уделяется реальные повседневные проблемы, которые могут возникнуть (OECD, 2014). Это согласование учебной программы PM с теоретическими основами PISA также дает больше возможностей ирландским учащимся работать на более высоком уровне, когда речь идет о таком стандартизированном тестировании и типах наборов навыков, которые необходимы для сохранения конкурентоспособности таким образом.В отчете PISA также подчеркивается необходимость того, чтобы учащиеся могли продемонстрировать процедурные факты и навыки в дополнение к применению математики в незнакомых ситуациях.
Зная теоретические основы проекта «Математика» и его частичное соответствие интерпретациям решения задач, предложенным PISA и Пойа (1945), ниже изложены средства, с помощью которых оценивалось решение задач в этом исследовании.
4. Выводы
4.1. Общая результативность группового диагностического теста и успеваемость по программе
Парная выборка t -тесты использовались для определения того, была ли вся группа студентов, прошедших диагностический тест ( n = 406), а также студенты в рамках отдельных программ показали статистически значимые результаты лучше в одном разделе теста по сравнению с другим.Все предположения для парных выборочных t-критериев были выполнены во всех случаях. Результаты показали, что была статистически значимая разница в средней успеваемости студентов в разделе A (x¯ = 65,54) по сравнению с разделом B ( = 40,54) диагностического теста, когда все студенты были проанализированы вместе ( p < ). 001), при этом средние показатели учащихся были статистически значимо лучше в разделе А, процедурном разделе диагностического теста (см. Таблицу 5).
Таблицу 5).
Было обнаружено, что один и тот же образец эффективности повторяется для каждой отдельной изученной программы независимо от уровня QQI (см. Таблицу 6).Было обнаружено, что средняя производительность каждой программы в разделе A, процедурном разделе, была статистически значимо лучше, чем средняя производительность в разделе B, разделе решения проблем ( p < 001). Из Таблицы 6 также видно, что те, кто поступил на программы с самым высоким уровнем QQI (уровень 8), как правило, имели более высокие результаты в обоих разделах теста, чем, например, те, кто поступил на 6-й уровень QQI. Есть одно исключение, в котором студенты, поступающие на инженерную программу QQI уровня 7, превзошли студентов, изучающих бизнес и фармацевтическое здравоохранение.Это может быть связано с более высоким математическим компонентом, связанным с инженерной программой, в отличие от двух других программ уровня 8 QQI.
Следует также отметить, что все программы, которые традиционно имеют более высокий математический компонент, связанный с ними (Инженерный QQI, уровень 7, Инженерный QQI, уровень 8 и Научный QQI, уровень 8), независимо от уровня QQI, набирают в среднем более 40 баллов. % в разделе B диагностического теста, который в ирландском контексте считается проходным баллом.Все остальные программы отстают: Pharmaceutical Healthcare чуть ниже проходного балла в 40% по разделу B.
% в разделе B диагностического теста, который в ирландском контексте считается проходным баллом.Все остальные программы отстают: Pharmaceutical Healthcare чуть ниже проходного балла в 40% по разделу B.
4.2. Показатели диагностических тестов в разбивке по полу
При изучении всей выборки ( n = 406) не обнаружено статистически значимой разницы в результатах мужчин и женщин ни в разделе A ( p = ,093), ни в разделе B ( p = .137) теста с мужчинами, имеющими несколько более высокие средние показатели по сравнению с женщинами.
Когда каждую программу исследовали отдельно с точки зрения результатов в каждом разделе диагностического теста в зависимости от пола, все программы, кроме двух, также не показали статистически значимой разницы между показателями пола ( p = .06). Два исключения наблюдались в программе Engineering QQI Level 7, где мужчины показали статистически значимо лучшие результаты, чем женщины, в разделе B теста ( p = ,04), при условии равной дисперсии. Другое исключение произошло в программе «Наука», где мужчины снова превзошли женщин с точки зрения средней эффективности в разделе A теста ( p = ,032), равные отклонения не предполагались.
Другое исключение произошло в программе «Наука», где мужчины снова превзошли женщин с точки зрения средней эффективности в разделе A теста ( p = ,032), равные отклонения не предполагались.
4.3. Результаты диагностического теста по возрастным группам
Данные, описанные в этом разделе и упомянутые в Таблице 7, относятся только к тем учащимся, которые прошли диагностический тест, а также проходили обучение по программам уровня 8 QQI.Обоснованием этого является то, что цифры были недостаточно большими для целей сравнения на любом из других уровней QQI по годам.
При изучении успеваемости учащихся в разделе А диагностического теста для сравнения успеваемости за год было принято допущение об однородности дисперсий ( p = .746). Таким образом, можно сообщить следующие результаты теста ANOVA: F (2,254) = 0,665, p = 0,515. Результаты показывают, что не было обнаружено статистически значимой разницы между средними показателями учащихся 8-го уровня QQI в разделе A теста за три исследуемых года.
Для раздела B диагностического теста допущение об однородности дисперсий не выполнялось ( p = ,03), поэтому был изучен дисперсионный анализ Уэльса, который оказался значимым ( p = ,023), и поэтому Были изучены результаты теста Games-Howell Post Hoc. Эти результаты показывают, что успеваемость учащихся в разделе B теста в 2017 г. была статистически значимо выше по сравнению с успеваемостью в 2018 и 2019 гг. ( p < 001 в обоих случаях).Однако разница между показателями 2018 и 2019 годов оказалась незначительной (95 168 p 95 169 = ,756). Вывод о статистически значимо более высокой успеваемости учащихся секции Б в 2017 г. следует рассматривать в свете того, что они представляют меньше учащихся, представляющих эту когорту ( n = 12) (см. Таблицу 7).
5. Обсуждение
Студенты, участвовавшие в этом исследовании, чрезвычайно разнообразны с точки зрения их дисциплин, оценок по математике при поступлении в высшие учебные заведения (которые основаны на успеваемости по математике в аттестате об окончании школы) и их общей успеваемости в аттестате об окончании школы. 2 Учащиеся второго уровня образования в Ирландии, тем не менее, все изучали одну и ту же учебную программу по математике проекта «Выпускной аттестат» (хотя и на разных уровнях; базовый, обычный или высший уровень математики) и столкнулись с альтернативным подходом к преподаванию и изучению математики, который был введена в систему образования второго уровня в 2010 году. Принимая во внимание все эти различия и сходства, результаты, представленные в этой статье, ясно подчеркивают статистически значимо более низкую успеваемость поступающих студентов бакалавриата в отношении навыков решения проблем по сравнению с процедурными навыками.
2 Учащиеся второго уровня образования в Ирландии, тем не менее, все изучали одну и ту же учебную программу по математике проекта «Выпускной аттестат» (хотя и на разных уровнях; базовый, обычный или высший уровень математики) и столкнулись с альтернативным подходом к преподаванию и изучению математики, который был введена в систему образования второго уровня в 2010 году. Принимая во внимание все эти различия и сходства, результаты, представленные в этой статье, ясно подчеркивают статистически значимо более низкую успеваемость поступающих студентов бакалавриата в отношении навыков решения проблем по сравнению с процедурными навыками.
Большое разнообразие вступительных стандартов по математике, а также различные дисциплины студентов из этой выборки позволяют всем заинтересованным сторонам в сфере образования получить обзор текущих уровней математических компетенций в высшем учебном заведении в целом. Это также предоставило платформу для потенциального выделения конкретных областей дисциплин, в которых поступающие учащиеся могли освоить навыки решения задач, на которых основное внимание уделяется образованию второго уровня, а также процедурные навыки, которые ранее доминировали в ирландском классе математики (Hourigan & O’Donoghue, 2007). ).Хотя студенты определенных программ на получение степени в среднем показали лучшие результаты, чем студенты программ на получение степени, менее ориентированных на математику, все группы показали статистически значимо худшие результаты в разделе B по сравнению с разделом A.
).Хотя студенты определенных программ на получение степени в среднем показали лучшие результаты, чем студенты программ на получение степени, менее ориентированных на математику, все группы показали статистически значимо худшие результаты в разделе B по сравнению с разделом A.
в прошлом было обнаружено, что мужчины превосходят женщин и наоборот в различных аспектах математических достижений в разных секторах образования (Guiso et al., 2008; Чжан и Манон, 2000). Однако в случае с этим исследованием это не играет существенной роли с точки зрения выявления каких-либо полезных или заслуживающих внимания сведений о процедурном решении задач в математике.
Что важно и примечательно в случае этих выводов, так это то, что по мере того, как Project Math становится все более укоренившимся в обычном преподавании и изучении математики второго уровня, предполагаемое улучшение результатов в решении математических задач, по-видимому, не наблюдается среди учащихся в широкий спектр дисциплин высшего образования. Это особенно важно, поскольку вопросы решения проблем в этом диагностическом тесте фактически являются зеркальным отображением процедурных вопросов с некоторым контекстом. Можно увидеть, что вопросы решения проблем, используемые в диагностическом тесте, относятся к менее экстремальному концу шкалы решения проблем, как описано McClure (2013), и все они возникли на экзаменах для младших классов и аттестатов.
Это особенно важно, поскольку вопросы решения проблем в этом диагностическом тесте фактически являются зеркальным отображением процедурных вопросов с некоторым контекстом. Можно увидеть, что вопросы решения проблем, используемые в диагностическом тесте, относятся к менее экстремальному концу шкалы решения проблем, как описано McClure (2013), и все они возникли на экзаменах для младших классов и аттестатов.
Возникает несколько вопросов для обсуждения:
Изменилось ли на практике преподавание и изучение математики на втором уровне и какой прогресс мы достигли, если таковой имеется?
Демонстрируют ли учащиеся «выученную беспомощность», когда дело доходит до математических задач, которые не являются исключительно процедурными?
Нужны ли более радикальные изменения в обучении решению задач, чтобы учащиеся действительно научились адаптироваться и работать с невидимыми задачами по математике?
Оказывает ли порядок, в котором мы обычно обучаем навыкам решения задач, неблагоприятное воздействие на навыки решения задач у учащихся?
Является ли это проблемой грамотности, а не решением математических задач?
5.
 1. Изменилось ли на практике преподавание и изучение математики на втором уровне, и какой прогресс мы добились, если таковой имеется?
1. Изменилось ли на практике преподавание и изучение математики на втором уровне, и какой прогресс мы добились, если таковой имеется? Хотя первоначальные ранние показатели студентов и преподавателей высших учебных заведений предполагали возможное улучшение навыков решения проблем и готовности участвовать в решении проблем (Prendergast et al., 2017; Treacy & Faulkner, 2015), это более всестороннее целенаправленное исследование проблемы студентов решение результатов при поступлении в высшие учебные заведения предполагает, что необходимо повторно исследовать эти ранние индикаторы, используя более строгие меры.Результаты этого исследования, которые не столь благоприятны с точки зрения математической успеваемости после введения PM, могут, тем не менее, демонстрировать, что изменения в учебной программе, подобные этим, требуют времени, чтобы все заинтересованные стороны действительно с ними справились (Prendergast & Treacy, 2018). и, возможно, еще слишком рано, чтобы увидеть какие-либо реальные изменения в успеваемости учащихся. Нужно помнить, что «спешить с реформой образования — значит ее губить» (Sahlberg, 2011, с. 3). В то время как учащиеся могут быть более открытыми, способными и готовыми использовать язык решения проблем и видеть необходимость/преимущества такого мастерства, продемонстрированные способности представляются отдельной проблемой.Это первый шаг к внедрению успешных изменений, т. е. оценка актуальности изменений и мотивация к участию в них (Lewin, 1948; Ryan et al., 2020).
Нужно помнить, что «спешить с реформой образования — значит ее губить» (Sahlberg, 2011, с. 3). В то время как учащиеся могут быть более открытыми, способными и готовыми использовать язык решения проблем и видеть необходимость/преимущества такого мастерства, продемонстрированные способности представляются отдельной проблемой.Это первый шаг к внедрению успешных изменений, т. е. оценка актуальности изменений и мотивация к участию в них (Lewin, 1948; Ryan et al., 2020).
Возможно, также необходимо учитывать, что, хотя тщательное рассмотрение было уделено планированию и внедрению учебной программы Проекта по математике, в стратегии был недостаток, если она была развернута без учета школьной культуры (Fullan, 2007). Считается, что для успешной реализации любого крупного изменения, такого как учебная программа по математике второго уровня Project Math, учебные заведения должны сделать человеческий фактор и четкое понимание академической культуры и субкультуры основным направлением деятельности (Kezar & Eckel, 2002). ; Райан и др., 2020; Сторберг-Уокер и Торрако, 2004 г.).
; Райан и др., 2020; Сторберг-Уокер и Торрако, 2004 г.).
5.2. Демонстрируют ли учащиеся «выученную беспомощность», когда речь идет о математических задачах, не являющихся исключительно процедурными?
Существует понятие, описанное в педагогической литературе как «выученная беспомощность», которую очень трудно преодолеть (Firmin et al., 2004). Он часто присутствует у младших школьников, а также у учащихся, которые не развили общие навыки, такие как мотивация, настойчивость и настойчивость в образовательном контексте.Решение проблем — это не только когнитивный процесс, но и включает в себя компонент отношения, в котором учащиеся должны быть заинтересованы в его выполнении, а также верить, что они могут добиться в нем успеха (Jonassen & Tessmer, 1996; Prendergast et al., 2018). В дополнение к потенциальной роли «выученной беспомощности», в международном контексте сообщалось, что неумение считаться с математикой является социально приемлемым (Ernest, 1995). Это не так в других дисциплинах, где считается очень неприемлемым признать, по крайней мере публично, что, например, вы не умеете читать или писать (Attard, 2016; Holden, 2013). Культура, связанная с математическими способностями, и распространенность «выученной беспомощности» могут быть комбинацией факторов, способствующих снижению успеваемости учащихся в области решения математических задач после завершения проекта «Математика» и поступления в высшие учебные заведения.
Культура, связанная с математическими способностями, и распространенность «выученной беспомощности» могут быть комбинацией факторов, способствующих снижению успеваемости учащихся в области решения математических задач после завершения проекта «Математика» и поступления в высшие учебные заведения.
5.3. Нужны ли более радикальные изменения в обучении решению задач, чтобы учащиеся действительно научились адаптироваться и работать с невидимыми задачами по математике?
Результаты этого исследования также заставили авторов задуматься о том, будет ли переход от учебной программы по математике второго уровня, которая была сосредоточена в основном на зубрежке и процедурных навыках, а также на навыках решения задач на менее экстремальном конце спектра определений. привести к каким-либо реальным изменениям? Навыки решения проблем, проверяемые на экзаменах Junior и Leaving Certificate, можно охарактеризовать как предсказуемые проблемы.Не пропустили ли учащиеся набор навыков, которые можно развить, занимаясь более экстремальным концом шкалы решения проблем? Исследования показали, что обучение процессу решения проблем, в отличие от участия в реальных проблемах, не улучшает производительность решения проблем (Бейер, 1984; Де Боно, 1983). Такие исследования показали, что овладение обобщенными навыками решения проблем не делает различий между сильными и слабыми решателями проблем, и утверждали, что наряду с решением подлинных проблем в реалистичных контекстах понимание контекста было наиболее важной чертой в том, чтобы стать хорошим решателем проблем.
Такие исследования показали, что овладение обобщенными навыками решения проблем не делает различий между сильными и слабыми решателями проблем, и утверждали, что наряду с решением подлинных проблем в реалистичных контекстах понимание контекста было наиболее важной чертой в том, чтобы стать хорошим решателем проблем.
5.4. Оказывает ли порядок, в котором мы склонны обучать навыкам решения задач процедурных стихов, неблагоприятное влияние на навыки решения задач учащихся?
Еще одно соображение, которое не фигурирует во многих дискуссиях о математических навыках учащихся второго уровня в Ирландии, заключается в том, что преобладающее внимание традиционно уделяется владению процедурными навыками, что привело к ситуации, в которой учащиеся не заинтересованы в понимании смысла. или обоснование навыков, которыми они владеют, с помощью процедурного подхода.Исследования, проведенные 20 лет назад, показывают, что это часто может иметь место, т. е. когда учащиеся овладевают процедурными навыками, у них почти нет мотивации исследовать их смысл или рассуждения или то, как они вписываются в более широкую картину (Hiebert, 1999). Как и в случае с проектом «Математика», мы должны продолжать видеть необходимость в том, чтобы учащиеся развивали как процедурную, так и понятийную беглость, но также осознавать, что развитие концептуального понимания учащимися процедурных навыков должно происходить или, по крайней мере, происходить в сочетании с преподаванием. и изучение процедур.Если бы мы могли увидеть критическую важность порядка, в котором должно происходить это преподавание и обучение, то успеваемость учащихся в обеих областях могла бы улучшиться. Это позволит учащимся развить глубокие и гибкие знания процедурных навыков, а также способность принимать решения о том, какие процедуры необходимы в каких ситуациях, что необходимо для успеха в математике и задачах прикладного математического контекста (NCTM, 2014a; NRC, 2001). , 2005, 2012; Звезда, 2005).
Как и в случае с проектом «Математика», мы должны продолжать видеть необходимость в том, чтобы учащиеся развивали как процедурную, так и понятийную беглость, но также осознавать, что развитие концептуального понимания учащимися процедурных навыков должно происходить или, по крайней мере, происходить в сочетании с преподаванием. и изучение процедур.Если бы мы могли увидеть критическую важность порядка, в котором должно происходить это преподавание и обучение, то успеваемость учащихся в обеих областях могла бы улучшиться. Это позволит учащимся развить глубокие и гибкие знания процедурных навыков, а также способность принимать решения о том, какие процедуры необходимы в каких ситуациях, что необходимо для успеха в математике и задачах прикладного математического контекста (NCTM, 2014a; NRC, 2001). , 2005, 2012; Звезда, 2005).
5.5. Является ли это проблемой грамотности, а не решением математических задач?
Последнее соображение для обсуждения в связи с результатами этого исследования заключается в том, что большая часть результатов с точки зрения решения задач может быть связана не с проблемами понимания математических концепций, а скорее с проблемами грамотности. Кое-что, о чем было написано и рассмотрено как на этапах планирования проекта «Математика», так и во время его развертывания, было следствием проблем с грамотностью для учащихся при изучении учебной программы, где сейчас спрос на грамотность гораздо выше, чем раньше ( Мерриман и др., 2014; Прендергаст и др., 2016). Многие учителя выражали обеспокоенность по поводу таких проблем на ранних этапах развертывания проекта «Математика», однако широко признано, что это необходимая задача, если ученики действительно хотят заниматься решением задач по математике (Foshay & Kirkley, 2003).Возможно, меры, принимаемые для решения этих проблем, требуют дальнейшего рассмотрения, чем они были назначены до сих пор, и вносят свой вклад в большую часть проблем, когда речь идет об улучшении математических навыков.
Кое-что, о чем было написано и рассмотрено как на этапах планирования проекта «Математика», так и во время его развертывания, было следствием проблем с грамотностью для учащихся при изучении учебной программы, где сейчас спрос на грамотность гораздо выше, чем раньше ( Мерриман и др., 2014; Прендергаст и др., 2016). Многие учителя выражали обеспокоенность по поводу таких проблем на ранних этапах развертывания проекта «Математика», однако широко признано, что это необходимая задача, если ученики действительно хотят заниматься решением задач по математике (Foshay & Kirkley, 2003).Возможно, меры, принимаемые для решения этих проблем, требуют дальнейшего рассмотрения, чем они были назначены до сих пор, и вносят свой вклад в большую часть проблем, когда речь идет об улучшении математических навыков.
6. Дальнейшие исследования и выводы
Основываясь на выводах, представленных в данной исследовательской статье, авторы приходят к выводу, что пришло время обратить внимание на качественный анализ. Это должно осуществляться в форме опроса студентов, начинающих обучение на бакалавриате (или тех, кто уже прошел диагностические тестовые экзамены, обсуждаемые в этом исследовании), чтобы определить, что есть/было в вопросах раздела А теста, которые более/менее привлекательны. сложные/более легкие для выполнения по сравнению с теми, которые представлены в разделе B.Понимание учащимися того, что может быть «ментальным блоком», когда дело доходит до успешного решения вопросов по решению проблем, было бы наиболее полезным для всех заинтересованных сторон в сфере образования. В качестве альтернативы можно было бы выяснить, осознают ли учащиеся разные и значительно более низкие результаты в одной математической области по сравнению с другой.
Это должно осуществляться в форме опроса студентов, начинающих обучение на бакалавриате (или тех, кто уже прошел диагностические тестовые экзамены, обсуждаемые в этом исследовании), чтобы определить, что есть/было в вопросах раздела А теста, которые более/менее привлекательны. сложные/более легкие для выполнения по сравнению с теми, которые представлены в разделе B.Понимание учащимися того, что может быть «ментальным блоком», когда дело доходит до успешного решения вопросов по решению проблем, было бы наиболее полезным для всех заинтересованных сторон в сфере образования. В качестве альтернативы можно было бы выяснить, осознают ли учащиеся разные и значительно более низкие результаты в одной математической области по сравнению с другой.
Зачастую неосведомленность студентов о своих сильных и слабых сторонах в какой-либо области дисциплины может негативно сказаться на прогрессе в высшем образовании (McMillan & Hearn, 2008).Понимают ли учащиеся, что вопросы в разделах A и B являются парными и, следовательно, требуют одинаковых математических навыков для успешного выполнения каждого вопроса? Учащихся можно спросить, что преподаватели математики могли бы сделать по-другому, чтобы поддерживать их лучше, чем они в настоящее время в этих областях. Что учащиеся могут предложить изменить с точки зрения математического образования второго и третьего уровня?
Что учащиеся могут предложить изменить с точки зрения математического образования второго и третьего уровня?
Может показаться, что это исследование поставило больше вопросов, чем дало ответов, однако авторы пришли к выводу, что ценные выводы были сделаны с точки зрения статистически значимо более слабой успеваемости учащихся в решении задач по сравнению с процедурными навыками в математике и пути к добраться до основной причины того, почему это может быть, было несколько вырезано.Ухудшение базовых математических навыков было хорошо задокументировано, и теперь задокументированы сравнительно более низкие показатели с точки зрения навыков решения задач, которые проект «Математика» намеревался улучшить. Поэтому настало время выяснить почему результатов этих лонгитюдных исследований, чтобы мы могли принять меры для лучшей поддержки наших студентов в улучшении математических областей, которые мы считаем необходимыми.
Как распознать дискалькулию — Институт детского разума
У многих детей проблемы с математикой, но у некоторых трудности выходят за рамки легкого разочарования. Если проблемы с математикой у вашего ребенка серьезные и постоянные, они могут быть признаком расстройства обучения, которое называется дискалькулия.
Если проблемы с математикой у вашего ребенка серьезные и постоянные, они могут быть признаком расстройства обучения, которое называется дискалькулия.
Что такое дискалькулия?
Дискалькулия — это термин, используемый для описания конкретных нарушений обучаемости, которые влияют на способность ребенка понимать, учиться и выполнять математические и числовые операции.
Насколько это распространено?
Хотя исследования распространенности ограничены, по оценкам, от 5 до 7% детей младшего школьного возраста могут страдать дискалькулией.Также в настоящее время считается, что дискалькулия встречается в равной степени у обоих полов.
Все ли математические трудности вызваны дискалькулией?
Нет. Не все трудности на уроках математики, даже серьезные, вызваны дискалькулией. Такие расстройства, как дислексия, зрительная или слуховая обработка, СДВГ и другие, также могут повлиять на способность ребенка соответствовать ожиданиям при решении математических задач. У детей с дискалькулией также могут быть другие трудности с обучением.Многие делают.
У детей с дискалькулией также могут быть другие трудности с обучением.Многие делают.
Связанный: Поддержка эмоциональных потребностей детей с ограниченными возможностями обучения
Что искать
Маленький ребенок с дискалькулией может:
- Имеют трудности с распознаванием цифр
- Задержка в обучении счету
- Попытка соединить числовые символы (5) с соответствующими им словами (пять)
- Испытываете трудности с распознаванием образов и расстановкой вещей по порядку
- Потерять счет при счете
- Потребность в использовании визуальных средств, таких как пальцы, помогает считать
А поскольку математика становится основной частью школьного дня, дети с дискалькулией, вероятно, будут:
- Имеют серьезные трудности с изучением основных математических функций, таких как сложение и вычитание, таблица умножения и многое другое
- Быть неспособным понять концепции текстовых задач и других нечисловых математических вычислений
- Трудно оценить, сколько времени потребуется для выполнения задачи
- Проблемы с домашними заданиями и тестами по математике
- С трудом успеваете по математике на уровне своего класса
- Борьба с обработкой визуально-пространственных идей, таких как графики и диаграммы
Воздействие дискалькулии не прекращается, когда уроки математики заканчиваются. Расстройство может также повлиять на детей вне школы. Дети с дискалькулией также:
Расстройство может также повлиять на детей вне школы. Дети с дискалькулией также:
- Проблемы с запоминанием чисел, таких как почтовые индексы, номера телефонов или результаты игр
- Борьба с денежными вопросами, такими как внесение сдачи, подсчет счетов, расчет чаевых, разделение чека или оценка того, сколько что-то будет стоить.
- Трудно оценить длину расстояний и время, которое потребуется, чтобы добраться из одного места в другое
- Попытки запомнить направление
- Трудно отличить слева направо
- Легко разочаровываются в играх, требующих постоянного ведения счета, стратегии с числами или счета
- Трудно читать часы и определять время
Заметный разрыв
Самым большим признаком определенного расстройства обучения является заметное несоответствие между способностями и способностями.Ребенок с дискалькулией может хорошо успевать по другим предметам, таким как английский язык или история, но иметь очень низкие оценки по математике и математическим предметам.
Как правильно называется дискалькулия?
В DSM-5 дискалькулия называется «специфической неспособностью к обучению с нарушением математики», но «дискалькулия» по-прежнему является общепринятым термином и используется школами и специалистами по обучению.
Как диагностируется дискалькулия?
Специфического теста на дискалькулию не существует.Выполнение следующих шагов может помочь вашему ребенку получить помощь и условия, в которых он нуждается.
- Обратитесь к врачу: Исключите любые медицинские проблемы, такие как нарушения слуха или зрения, которые могут повлиять на процесс обучения вашего ребенка.
- Проконсультируйтесь со своим учителем: Попросите учителя математики вашего ребенка отметить области, в которых у него больше всего проблем, и все стратегии, которые могут помочь.
- Спросите о других областях: Подсчитано, что половина детей с дискалькулией также имеют другие проблемы с обучением.
 Понимание полного профиля обучения вашего ребенка поможет вам отстаивать его потребности
Понимание полного профиля обучения вашего ребенка поможет вам отстаивать его потребности - Проконсультируйтесь со специалистом: После того, как вы подготовились, поговорите со специалистом в области обучения, который может оценить вашего ребенка и дать вам конкретный отзыв о том, как помочь.
математических и французских тестов | Педагогический факультет
Промежуточный базовый тест на знание математики
Для зачисления на дополнительный базовый курс средней квалификации (математика) зарегистрированные лица, не завершившие ДВА полных университетских зачетных курса по математике (т.е. исчисление, геометрия, линейная алгебра, статистика) необходимы для успешного прохождения нашего промежуточного теста на знание базовой математики, проводимого через Управление профессионального обучения, прежде чем быть допущенным к курсу AQ.
Этот тест:
- вводится после регистрации; заявители уведомляются по электронной почте
- заполняется онлайн
- состоит из набора вопросов с несколькими вариантами ответов, рассчитанных по времени
- требует минимальной оценки 60% (C), чтобы иметь право на поступление к обращениям.
 Разрешена одна попытка тестирования за сессию.
Разрешена одна попытка тестирования за сессию.Неподходящие кандидаты могут выбрать:
- Перевод на другой курс ИЛИ,
- Отказ от участия для получения полного возмещения за вычетом невозмещаемой суммы тестового и регистрационного взносов.
Тест на знание французского языка
Чтобы зарегистрироваться на дополнительную квалификацию по части 1 французского языка как второго, зарегистрированные лица должны успешно пройти тест на знание французского языка, проводимый Управлением профессионального обучения, прежде чем быть допущенным к курсу AQ.
Тест:
- вводится после регистрации; кандидаты уведомляются по электронной почте
- включает онлайн-компонент, разделенный на письменные категории, понимание прочитанного, грамматику и устные категории
- требует уровня владения языком 3 или 4 в каждой категории для прохождения вступительного теста
Все результаты теста являются окончательными и не подлежат проверке к обращениям.




 pdf
pdf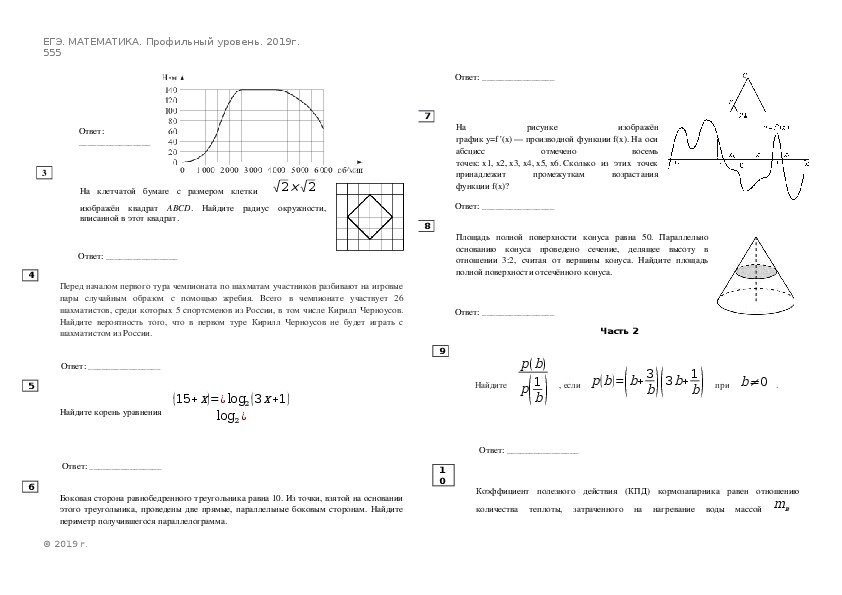 (DES, 2017, стр. 5)
(DES, 2017, стр. 5) Понимание полного профиля обучения вашего ребенка поможет вам отстаивать его потребности
Понимание полного профиля обучения вашего ребенка поможет вам отстаивать его потребности Разрешена одна попытка тестирования за сессию.
Разрешена одна попытка тестирования за сессию.