Олимпиада ломоносова математика: Олимпиада «Ломоносов» | Математика | Физика

Особые права и преимущества, обусловленные уровнями олимпиад — филиал в г. Пенза

40. Право на прием без вступительных испытаний имеют:

а) победители и призеры заключительного этапа всероссийской олимпиады школьников (далее – победители и призеры всероссийской олимпиады), члены сборных команд Российской Федерации, участвовавших в международных олимпиадах по общеобразовательным предметам и сформированных в порядке, установленном федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно–правовому регулированию в сфере образования (далее – члены сборных команд Российской Федерации), по специальностям и (или) направлениям подготовки, соответствующим профилю всероссийской олимпиады школьников или международной олимпиады – в течение 4 лет, следующих за годом проведения соответствующей олимпиады;

б) победители и призеры IV этапа всеукраинских ученических олимпиад, члены сборных команд Украины, участвовавших в международных олимпиадах по общеобразовательным предметам, по специальностям и (или) направлениям подготовки, соответствующим профилю всеукраинской ученической олимпиады или международной олимпиады, – в течение 4 лет, следующих за годом проведения соответствующей олимпиады, если указанные победители, призеры и члены сборных команд относятся к числу лиц к числу лиц, указанных в части 3.

1 статьи 5 Федерального закона № 84–ФЗ.

45. Победителям и призерам олимпиад школьников, проводимых в порядке, устанавливаемом федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно–правовому регулированию в сфере образования (далее – олимпиады школьников), в течение 4 лет, следующих за годом проведения соответствующей олимпиады, Университетом предоставляются следующие особые права при приеме на обучение по программам бакалавриата и программам специалитета по специальностям и (или) направлениям подготовки, соответствующим профилю олимпиады школьников:

1) прием без вступительных испытаний на обучение по программам бакалавриата и программам специалитета по специальностям и направлениям подготовки, соответствующим профилю олимпиады школьников;

2) быть приравненными к лицам, набравшим максимальное количество баллов ЕГЭ по общеобразовательному предмету, соответствующему профилю олимпиады школьников (далее – право на 100 баллов).

Особые права, указанные в подпунктах 1 и 2 настоящего пункта, могут предоставляться одним и тем же поступающим. В случае предоставления особого права, указанного в подпункте 2 настоящего пункта, поступающим устанавливается наивысший результат (100 баллов) соответствующего вступительного испытания (испытаний).

46. Лицам, указанным в пунктах 42 и 45 настоящих Правил, предоставляется в течение сроков, указанных в пунктах 42 и 45 настоящих Правил  преимущество посредством приравнивания к лицам, набравшим максимальное количество баллов ЕГЭ (100 баллов) по общеобразовательному предмету, если общеобразовательный предмет соответствует профилю олимпиады.

47. Для предоставления победителям и призерам олимпиад школьников особых прав и преимуществ, указанных в пунктах 45 и 46 настоящих Правил Университет устанавливает в Приложении № 12 к настоящим Правилам уровень и перечень олимпиад, по которым представляется каждое из указанных прав и преимуществ, а также определяет в данном Приложении по каждой олимпиаде (по каждому уровню олимпиад), за какие классы обучения по общеобразовательной программе должны быть получены результаты победителя (призера) для предоставления соответствующего особого права или преимущества.

Особое право или преимущество, предоставляемое призерам олимпиады школьников, предоставляется также победителям этой олимпиады.

48. Для предоставления особых прав, указанных в подпункте «а» и «б» пункта 42 и пункте 45 настоящих Правил, и преимущества, указанного в пункте 46 настоящих Правил, Университет самостоятельно устанавливает соответствие профиля олимпиад специальностям и направлениям подготовки, а также соответствие профиля олимпиад (статуса чемпиона (призера) в области спорта) общеобразовательным предметам в Приложении №12 к настоящим Правилам

49. При приеме на обучение по одной образовательной программе особые права, предусмотренные пунктами 42 и 45 настоящих Правил, и преимущество, предусмотренное пунктом 46 настоящих Правил, не могут различаться при приеме для обучения в Университет и для обучения в его филиале, при приеме на различные формы обучения, а также при приеме на места в пределах особой квоты, на основные места в рамках контрольных цифр и на места по договорам об оказании платных образовательных услуг.

50. Особые права, указанные в пункте 45 настоящих Правил, и преимущество, указанное в пункте 46 настоящих Правил, предоставляются победителям и призерам олимпиад школьников при наличии у них результатов ЕГЭ не ниже количества баллов, установленного приказом Ректора:

— для использования особого права, указанного в подпункте 1 пункта 45 настоящих Правил – по общеобразовательному предмету, соответствующему профилю олимпиады.

Указанный общеобразовательный предмет выбирается Университетом из числа общеобразовательных предметов, соответствующих профилю олимпиады, установленных в перечне олимпиад школьников, утверждаемом федеральным органом исполнительной власти, осуществляющим функции по выработке государственной политики и нормативно–правовому регулированию в сфере образования, а в случае, если в указанном перечне не установлены общеобразовательные предметы, по которым проводится ЕГЭ, – устанавливается Университетом самостоятельно.

— для использования особого права, указанного в подпункте 2 пункта 45 настоящих Правил, или преимущества, указанного в п. 46 настоящих Правил, – по общеобразовательному предмету, соответствующему вступительному испытанию.

Университет устанавливает указанное количество баллов в размере 75 баллов.

Перечень соответствия образовательных программ, общеобразовательных вступительных испытаний профилям всероссийских и международных олимпиад, по которым предоставляются особые права

Перечень олимпиад школьников, по результатам которых предоставляются особые права

Три медали завоевали школьники из Москвы на Международной математической олимпиаде

Московские школьники выиграли три медали на 62-й Международной математической олимпиаде. Золотыми медалями награждены Данил Сибгатуллин из школы № 1589 и Айдар Ибрагимов из СУНЦ МГУ. Серебро завоевал Андрей Шевцов из лицея «Вторая школа». Сергей Собянин поздравил школьников на своей странице в социальной сети «ВКонтакте». 

 

Олимпиада проходила с 14 по 24 июля в онлайн-формате, ее участниками стали школьники из более чем 100 стран. Всего на счету сборной России шесть медалей: пять золотых и одна серебряная. Благодаря этому результату страна заняла второе место в неофициальном командном зачете. Полные результаты сборной опубликованы на сайте Минпросвещения России.  

Организатором олимпиады в этом году стал Санкт-Петербург. Состязание включало в себя два тура, в каждом из которых было по три задачи. Они затронули разные области школьной математики: геометрию, теорию чисел, алгебру и комбинаторику. Помимо соревновательной части, в программу вошли лекции и онлайн-экскурсии.

Международная математическая олимпиада проводится с 1959 года. Каждую страну представляет команда, состоящая не более чем из шести школьников. Итоги соревнования подводятся в личном зачете, а по сумме баллов участников формируется неофициальный командный рейтинг.

В Москве уделяют пристальное внимание поддержке и развитию математического образования. Популяризации математики способствуют кружки и олимпиады, такие как «Математический праздник», турнир имени М.В. Ломоносова и Всероссийская олимпиада школьников.

Юным москвичам, которые интересуются математикой, помогает и проект «Математическая вертикаль». Он дает ребятам многоцелевую предпрофильную подготовку по математике и в ее смежных областях, что позволяет школьникам раньше определиться с направлением будущего образования и работы и в дальнейшем стать востребованными специалистами, необходимыми городу.

Олимпиада по математике 2019-20 • Формула Единства

К уча­стию в олим­пиа­де при­гла­ша­ют­ся школь­ни­ки 5–11 клас­сов из Рос­сии и соот­вет­ству­ю­щих клас­сов из всех стран мира.  Уча­стие в олим­пиа­де бес­плат­ное.

Олим­пи­а­да вклю­че­на в пере­чень РСОШ (2 уро­вень). При­зё­ры олим­пи­а­ды полу­ча­ют пра­во на льгот­ную путёв­ку в лет­ний обра­зо­ва­тель­ный лагерь «Фор­му­ла Единства».

Орга­ни­за­то­ры олим­пи­а­ды в 2019/20

Парт­нер олим­пи­а­ды — Интел­лек­ту­аль­ный клуб «Сиг­ма».

Кон­так­ты орг­ко­ми­те­та олимпиады

Офи­ци­аль­ные документы

Награж­де­ние побе­ди­те­лей и призёров

В свя­зи с эпи­де­мио­ло­ги­че­ской обста­нов­кой, свя­зан­ной с пан­де­ми­ей коро­на­ви­ру­са, очно­го награж­де­ния побе­ди­те­лей и при­зе­ров в этом учеб­ном году не будет.

Дипло­мы побе­ди­те­лей и при­зё­ров из стран СНГ будут высла­ны на элек­трон­ные адре­са участ­ни­ков и реги­о­наль­ных пло­ща­док, на кото­рых про­во­дил­ся заклю­чи­тель­ный этап олим­пи­а­ды. Одно­вре­мен­но на эти адре­са будут высла­ны дипло­мы при­зё­ров сре­ди вне­кон­курс­ных участников.

Элек­трон­ные вер­сии дипло­мов уже доступ­ны для ска­чи­ва­ния на сай­те Рос­сий­ско­го сове­та олим­пи­ад школь­ни­ков. Если элек­трон­ная вер­сия дипло­ма отсут­ству­ет или есть ошиб­ка в дан­ных, про­сим неза­мед­ли­тель­но напи­сать об этом в оргкомитет.

Напо­ми­на­ем, что выда­чу сер­ти­фи­ка­тов участ­ни­ков и дипло­мов за побе­ду в отбо­роч­ном эта­пе регла­мент олим­пи­а­ды не предусматривает.

---

Хронология событий

Все новости олимпиады будут публиковаться ниже от более новых к более старым.

В соот­вет­ствии с Поряд­ком про­ве­де­ния олим­пи­ад школь­ни­ков, утвер­ждён­ным При­ка­зом Мино­бр­на­у­ки Рос­сии от 4 апре­ля 2014 г. №267, здесь опуб­ли­ко­ва­ны олим­пи­ад­ные рабо­ты побе­ди­те­лей и при­зё­ров олим­пи­а­ды «Фор­му­ла Един­ства» / «Тре­тье тыся­че­ле­тие» по мате­ма­ти­ке 2019/20 г.

Пуб­ли­ку­ем ито­го­вые резуль­та­ты заклю­чи­тель­но­го этапа.

При нали­чии ошиб­ки в лич­ных дан­ных про­сим неза­мед­ли­тель­но сооб­щить об этом в орг­ко­ми­тет по адре­су [email protected]​formulo.​org.

Инфор­ма­ция о награж­де­нии побе­ди­те­лей и при­зё­ров будет опуб­ли­ко­ва­на позднее.

Пуб­ли­ку­ем пред­ва­ри­тель­ные резуль­та­ты (обнов­ле­но вече­ром 30.03) и реше­ния задач заклю­чи­тель­но­го этапа:

Обра­ща­ем внимание:

• Каж­дый класс рас­по­ло­жен на отдель­ном листе.
• Вне­кон­курс­ные участ­ни­ки отме­че­ны  жел­тым цве­том .

Не позд­нее 23:59 28 мар­та по мос­ков­ско­му вре­ме­ни участ­ни­ки могут запро­сить рабо­ту и/​или подать апел­ля­цию (запрос на пере­смотр реше­ния опре­де­лён­ной зада­чи). Для это­го нуж­но при­слать пись­мо на адрес жюри ([email protected]​formulo.​org), ука­зав в теме пись­ма номер клас­са. В тек­сте пись­ма напи­ши­те «Запрос рабо­ты» или «Апел­ля­ция по зада­че №…», ука­жи­те свои фами­лию и имя. Обра­ти­те вни­ма­ние, что в резуль­та­те апел­ля­ции бал­лы за реше­ние могут как уве­ли­чить­ся, так и снизиться.

Если Вы обна­ру­жи­ли, что резуль­та­ты участ­ни­ка заклю­чи­тель­но­го эта­па отсут­ству­ют или есть ошиб­ка в пер­со­наль­ных дан­ных, про­сим без­от­ла­га­тель­но сооб­щить об этом в жюри.

Реше­ние о при­суж­де­нии дипло­мов будет при­ня­то при под­ве­де­нии окон­ча­тель­ных ито­гов (31 мар­та 2 апреля).

Ува­жа­е­мые участники!

Про­сим вас озна­ко­мить­ся с таб­ли­цей «Участ­ни­ки заклю­чи­тель­но­го эта­па», опуб­ли­ко­ван­ной ниже. Там в послед­нем столб­це ука­за­на пло­щад­ка, на кото­рую Вы при­гла­ше­ны. Спи­сок пло­ща­док с адре­са­ми опуб­ли­ко­ван рядом в отдель­ном фай­ле. Если Вы пла­ни­ру­е­те писать олим­пи­а­ду на пло­щад­ке, отлич­ной от ука­зан­ной для Вас, про­сим сооб­щить об этом в орг­ко­ми­тет до 20 февраля

Участ­ни­ки долж­ны иметь при себе удо­сто­ве­ре­ния лич­но­сти (пас­порт, сви­де­тель­ство о рож­де­нии или уче­ни­че­ский билет). Так­же необ­хо­ди­мо иметь с собой руч­ки и запас чистой бумаги.

Сове­ту­ем так­же взять с собой воду — про­дол­жи­тель­ность олим­пи­а­ды 4 часа.

Участ­ни­ки долж­ны будут запол­нить и при­ло­жить к рабо­те анке­ту, кото­рая будет выда­на им одно­вре­мен­но с зада­ча­ми. При этом на листах бума­ги с реше­ни­я­ми задач не долж­ны ука­зы­вать­ся фами­лия, имя и дру­гие пер­со­наль­ные данные.
Если Вы граж­да­нин РФ, явля­е­тесь при­зе­ром или побе­ди­те­лем про­шло­го года и не при­ни­ма­ли уча­стие в отбо­роч­ном эта­пе это­го года, Вашим роди­те­лям нуж­но запол­нить и под­пи­сать согла­сие на обра­бот­ку пер­со­наль­ных дан­ных (его нуж­но будет взять с собой и отдать организаторам).

Во вре­мя про­ве­де­ния эта­па не раз­ре­ша­ет­ся поль­зо­вать­ся спра­воч­ной лите­ра­ту­рой, учеб­ни­ка­ми и задач­ни­ка­ми, каль­ку­ля­то­ра­ми, ком­пью­те­ра­ми, мобиль­ны­ми теле­фо­на­ми и дру­ги­ми сред­ства­ми связи.

Реко­мен­ду­ем участ­ни­кам прий­ти за 20–30 минут до нача­ла, что­бы най­ти нуж­ное поме­ще­ние и запол­нить анкету.

Орг­ко­ми­тет про­сит участ­ни­ков и педа­го­гов не раз­ме­щать усло­вия задач в интер­не­те до 14 марта.

Пред­ва­ри­тель­ные ито­ги заклю­чи­тель­но­го эта­па будут опуб­ли­ко­ва­ны на сай­те про­грам­мы «Фор­му­ла Един­ства» не позд­нее 24 мар­та 25 мар­та 2020 г. Апел­ля­ции могут пода­вать­ся в тече­ние трёх дней после пуб­ли­ка­ции пред­ва­ри­тель­ных итогов.

На вся­кий слу­чай, во избе­жа­ние накла­док, свя­зан­ных с каран­ти­ном, про­сим за день до олим­пи­а­ды допол­ни­тель­но про­ве­рить инфор­ма­цию о спис­ке пло­ща­док на этой странице.

В насто­я­щее вре­мя спи­сок пло­ща­док заклю­чи­тель­но­го эта­па ещё уточ­ня­ет­ся, и рас­сыл­ка инфор­ма­ции для участ­ни­ков состо­ит­ся позд­нее (не поз­же 16 фев­ра­ля). При­но­сим изви­не­ния за воз­мож­ные неудобства.

Ува­жа­е­мые участ­ни­ки олим­пи­а­ды и их роди­те­ли! Пуб­ли­ку­ем пол­ный спи­сок школь­ни­ков (обнов­лен 22.02 в 20:41), при­гла­шен­ных на заклю­чи­тель­ный этап олим­пи­а­ды (он вклю­ча­ет в себя участ­ни­ков, про­шед­ших отбо­роч­ный этап в 2019/20 году, и призеров/​победителей олим­пи­а­ды 2018/19 года). Обра­ти­те вни­ма­ние, что участ­ни­ки из раз­ных клас­сов пока­за­ны на раз­ных листах файла!

Заклю­чи­тель­ный этап олим­пи­а­ды в Рос­сии прой­дёт 24 фев­ра­ля на реги­о­наль­ных пло­щад­ках. Нача­ло в 11:00 по мест­но­му вре­ме­ни, про­дол­жи­тель­ность 4 часа. На отдель­ных пло­щад­ках вре­мя нача­ла может быть иным (см. спи­сок пло­ща­док —  обнов­лен 22.02 в 17:23). Реко­мен­ду­ем участ­ни­кам прий­ти за 20–30 минут до нача­ла, что­бы най­ти нуж­ное поме­ще­ние и запол­нить анкету.

Сей­час мы пуб­ли­ку­ем пред­ва­ри­тель­ные спис­ки пло­ща­док; в него могут вно­сить­ся изме­не­ния и допол­не­ния, поэто­му мы стро­го реко­мен­ду­ем про­ве­рить инфор­ма­цию за день до про­ве­де­ния заклю­чи­тель­но­го эта­па. 11 или 12 фев­ра­ля мы будем делать рас­сыл­ку каж­до­му из участ­ни­ков о месте про­ве­де­ния олим­пи­а­ды, сле­ди­те за пись­ма­ми (ино­гда они могут попа­дать в спам!)

Пред­по­ла­га­ет­ся, что каж­дый участ­ник заклю­чи­тель­но­го эта­па при­хо­дит на пло­щад­ку, ука­зан­ную для него. Воз­мож­но уча­стие на дру­гой пло­щад­ке при усло­вии пред­ва­ри­тель­но­го согла­со­ва­ния с Оргкомитетом.

Заклю­чи­тель­ный этап олим­пи­а­ды будет про­во­дить­ся 24 фев­ра­ля 2020 г. на реги­о­наль­ных площадках.

Пло­щад­ки орга­ни­зу­ют­ся в боль­шин­стве реги­о­нов РФ и в дру­гих стра­нах, где про­жи­ва­ют участ­ни­ки заклю­чи­тель­но­го этапа.

Адре­са пло­ща­док и спис­ки участ­ни­ков будут опуб­ли­ко­ва­ны 1 фев­ра­ля на этой странице.

Рады сооб­щить, что в этом году в отбо­роч­ном эта­пе при­ня­ли уча­стие око­ло 4000 школь­ни­ков из 30 стран. К уча­стию в заклю­чи­тель­ном эта­пе при­гла­ше­ны школь­ни­ки, набрав­шие сум­мар­ный балл не менее:

Класс:	5	6	7	8	9	10	11
Балл:	24	25	33 30	19	18	25	31

Если Вы при­ни­ма­ли уча­стие в олим­пиа­де и Ваши резуль­та­ты отсут­ству­ют в таб­ли­це, не позд­нее 15 янва­ря Вам нуж­но было сооб­щить нам об этом. При этом про­сим ука­зать пол­ные анкет­ные дан­ные (ФИО, насе­лён­ный пункт, шко­лу, класс), спо­соб отправ­ки рабо­ты, элек­трон­ный адрес (ука­зан­ный при реги­стра­ции или исполь­зо­ван­ный при отправ­ке работы).

Дан­ные за раз­ные парал­ле­ли при­ве­де­ны на раз­ных листах фай­ла, резуль­та­ты упо­ря­до­че­ны по стра­нам и фами­ли­ям участ­ни­ков. Участ­ни­ки, набрав­шие необ­хо­ди­мое коли­че­ство бал­лов, отме­че­ны жел­тым цве­том.

Орг­ко­ми­тет готов испра­вить все обна­ру­жен­ные тех­ни­че­ские ошиб­ки. Если Вы обна­ру­жи­ли ошиб­ку в Ваших пер­со­наль­ных дан­ных, про­сим сроч­но напи­сать об этом в орг­ко­ми­тет по элек­трон­ной почте [email protected]​formulo.​org.

До встре­чи на заклю­чи­тель­ном эта­пе 24 февраля!

Орг­ко­ми­тет олим­пи­а­ды закон­чил ана­ли­зи­ро­вать посту­пив­шие заяв­ки и рабо­ты, и, в свя­зи с имев­ши­ми­ся тех­ни­че­ски­ми труд­но­стя­ми во вре­мя отбо­роч­но­го эта­па, выслал инфор­ма­ци­он­ные пись­ма всем участ­ни­кам.

Пожа­луй­ста, про­верь­те почту, кото­рую Вы ука­за­ли при отправ­ке решений!

P.S. Если Вам не при­хо­ди­ло ника­ких писем, как мож­но ско­рее свя­жи­тесь с Орг­ко­ми­те­том по элек­трон­ной почте [email protected]​formulo.​org!

При­ем работ от рос­сий­ских участ­ни­ков отбо­роч­но­го эта­па олим­пи­а­ды «Фор­му­ла Единства»/«Третье тыся­че­ле­тие» завер­шен. Жюри при­сту­па­ет к обра­бот­ке и про­вер­ке работ.

Уве­дом­ле­ния о полу­че­нии реше­ний долж­ны дой­ти всем участ­ни­кам в тече­ние несколь­ких дней. В ином слу­чае орг­ко­ми­тет допол­ни­тель­но свя­жет­ся с Вами по ука­зан­но­му элек­трон­но­му адресу.

Спа­си­бо за уча­стие! Пред­ва­ри­тель­ные резуль­та­ты будут в декабре.

Ува­жа­е­мые участ­ни­ки олимпиады!

В свя­зи с боль­шой нагруз­кой на сер­вер уве­дом­ле­ния о полу­че­нии Ваших работ со вче­раш­не­го вече­ра запаздывают 🙁

При­но­сим свои искрен­ние изви­не­ния и про­сим набрать­ся терпения.

P.S. Даже в самом страш­ном слу­чае, если Ваши реше­ния все-таки поте­ря­ют­ся, мы уви­дим Вашу реги­стра­цию и после окон­ча­ния эта­па допол­ни­тель­но свя­жем­ся с прось­бой зано­во их выслать.

Доро­гие участ­ни­ки олимпиады!

Исклю­чи­тель­но для вас было реше­но отсро­чить повы­ше­ние базо­вой сто­и­мо­сти уча­стия в зим­них сме­нах «Фор­му­лы Един­ства» 2020 в д. Гар­бо­ло­во и г. Гелен­джи­ке до 16 нояб­ря вклю­чи­тель­но при пода­че заяв­ки на мате­ма­ти­ку (в том чис­ле и олимпиадную)!

Все подроб­но­сти смот­ри­те в анон­сах смен:

Перед Вами зада­чи отбо­роч­но­го эта­па олимпиады.

Помни­те, что реше­ние зада­чи долж­но вклю­чать не толь­ко пра­виль­ный ответ, но и пол­ное обос­но­ва­ние это­го отве­та. Мы будем рады, если в олим­пиа­де при­мут уча­стие Ваши дру­зья, кото­рым нра­вит­ся мате­ма­ти­ка. Одна­ко рабо­ты с при­зна­ка­ми спи­сы­ва­ния и «кол­лек­тив­но­го твор­че­ства» рас­смат­ри­вать­ся не будут.

Усло­вия задач в рабо­ту пере­пи­сы­вать не нуж­но. Рабо­та может быть напи­са­на на англий­ском, укра­ин­ском, гру­зин­ском, испан­ском, немец­ком, пер­сид­ском, румын­ском, рус­ском, казах­ском, узбек­ском, фран­цуз­ском, тай­ском, турец­ком язы­ке или эспе­ран­то. Исполь­зо­ва­ние дру­гих язы­ков долж­но быть зара­нее согла­со­ва­но с организаторами.

При­зё­ры меж­ду­на­род­ной мате­ма­ти­че­ской олим­пи­а­ды «Фор­му­ла Един­ства» / «Тре­тье тыся­че­ле­тие» 2018/19 г. будут при­гла­ше­ны непо­сред­ствен­но на заклю­чи­тель­ный этап.

Усло­вия задач

Поря­док отправ­ки реше­ний через интернет

Для уча­стия в мате­ма­ти­че­ской олим­пиа­де «Фор­му­ла Един­ства» / «Тре­тье тыся­че­ле­тие» 2019/20 необ­хо­ди­мо в срок до 12 нояб­ря 2019 г. вклю­чи­тель­но под­го­то­вить файл с реше­ни­я­ми задач и отпра­вить его через спе­ци­аль­ную анкету.

Загру­зить мож­но как тек­сто­вые фай­лы (в фор­ма­тах TXT, DOC, DOCX или PDF), так и ска­ны бумаж­ных работ (в фор­ма­тах JPG и PNG). Общее коли­че­ство фай­лов не долж­но пре­вы­шать 10. В фай­лах с реше­ни­я­ми задач не долж­ны ука­зы­вать­ся фами­лия, имя и дру­гие лич­ные дан­ные участника!

Вни­ма­ние! Не раз­ре­ша­ет­ся исполь­зо­вать одни реги­стра­ци­он­ные дан­ные для отправ­ки работ несколь­ких участ­ни­ков. Если Вы — учи­тель и хоти­те отпра­вить рабо­ты несколь­ких уче­ни­ков, напи­ши­те об этом в орг­ко­ми­тет, мы пред­ло­жим удоб­ный спо­соб сде­лать это.

Поря­док отправ­ки реше­ний в бумаж­ном виде

В каче­стве исклю­че­ния мож­но отпра­вить свою рабо­ту в жюри в бумаж­ном виде. К рабо­те долж­ны при­ла­гать­ся на отдель­ных листах запол­нен­ная анке­та участ­ни­ка и под­пи­сан­ное одним из роди­те­лей согла­сие на обра­бот­ку пер­со­наль­ных данных:

На самой рабо­те не долж­ны ука­зы­вать­ся лич­ные дан­ные участника.

Если в Вашем насе­лён­ном пунк­те есть мест­ный орг­ко­ми­тет, рабо­ту мож­но пере­дать в мест­ный орг­ко­ми­тет не позд­нее 12 нояб­ря (спи­сок мест­ных орг­ко­ми­те­тов будет опуб­ли­ко­ван в бли­жай­шее время).

Участ­ни­ки из насе­лён­ных пунк­тов, где нет мест­но­го орг­ко­ми­те­та, отправ­ля­ют свою рабо­ту и при­ла­га­е­мые доку­мен­ты в цен­траль­ный орг­ко­ми­тет по адре­су: 191023, С.-Петербург, наб. р. Фон­тан­ки, 27, С.-Петербургское отде­ле­ние Мате­ма­ти­че­ско­го инсти­ту­та им. В. А. Стек­ло­ва РАН, Орг­ко­ми­тет олим­пи­а­ды «Фор­му­ла Един­ства» / «Тре­тье тысячелетие».

Вопро­сы?

Все вопро­сы Орг­ко­ми­те­ту по усло­ви­ям задач и о поряд­ке про­ве­де­ния Олим­пи­а­ды мож­но задать по элек­трон­ной почте [email protected]​formulo.​org или по теле­фо­ну +7 (969) 717–41-93.

Еже­год­но объ­еди­нён­ная меж­ду­на­род­ная мате­ма­ти­че­ская олим­пи­а­да «Фор­му­ла Единства»/«Третье тыся­че­ле­тие» про­во­дит­ся в два этапа.

Отбо­роч­ный этап

Отбо­роч­ный этап явля­ет­ся заоч­ным. В этом году прой­дёт с 15 октяб­ря по 12 нояб­ря.

Подроб­ная инфор­ма­ция появит­ся бли­же к стар­ту эта­па. Не забудь­те под­пи­сать­ся на нашу рас­сыл­ку, что­бы полу­чить уведомление 🙂

Заклю­чи­тель­ный этап

Заклю­чи­тель­ный же этап — очный и, ори­ен­ти­ро­воч­но, состо­ит­ся в фев­ра­ле 2020 года. Подроб­ная инфор­ма­ция о местах про­ве­де­ния появит­ся зимой.

В июле стартовали международные олимпиады по математике, физике и биологии

В июле 2021 года проходят три международные олимпиады для школьников: по математике, биологии и физике.

Все члены команд – многократные участники программ «Сириуса», сборы кандидатов по этим предметам проходили в том числе в Образовательном центре. 

Математика

62-я Международная математическая олимпиада проходит с 18 июля в дистанционном формате, в ней участвуют более 100 стран. Россия два года подряд является организатором соревнований: в 2021 году открытие олимпиады состоялось в Санкт-Петербурге. В 2020 году Россия заняла второе место среди всех стран-участников в неофициальном командном зачете. 

В этом году в отечественной команде шестеро школьников: Айдар Ибрагимов, Андрей Шевцов и Данил Сибгатуллин из Москвы, Иван Бахарев и Максим Туревский из Санкт-Петербурга, Матвей Исупов из Удмуртии. Руководитель сборной  – учитель математики Президентского физико-математического лицея № 239 Санкт-Петербурга Кирилл Сухов, заместители – педагоги московского Центра педагогического мастерства Владимир Брагин и Андрей Кушнир. Результаты объявят на онлайн-церемонии 24 июля.

Физика

17 июля стартовала Международная физическая олимпиада, страна-организатор –  Литва. Олимпиада состоит из двух туров: в первом участники решают теоретические задачи, а во втором выполняют лабораторную работу. В 2020 году российские участники завоевали четыре золотых и серебряную медаль.

В команде России пять участников: Матвей Князев, Николай Кононенко, Денис Исмагилов, Артемий Новиков и Данила Самоделкин –  все из Москвы и Московской области. Сборной руководит проректор по учебной работе Московского физико-технического института Артем Воронов, его заместители – доцент МФТИ Михаил Осин, заместитель заведующего учебно-методический лабораторией по работе с одаренными детьми МФТИ Виталий Шевченко и тьютор этой же лаборатории Юрий Скаков. Победители соревнований будут известны 24 июля.

Биология

В Международной биологической олимпиаде, которую проводит Португалия, участвуют четверо российских ребят. Они выполнят практические и теоретические задания на базе МГУ имени М. В. Ломоносова. В прошлом году на онлайн-турнире по биологии IBO challenge, который заменил традиционную биологическую олимпиаду, россияне получили три золота и серебро.

В отечественную команду в этом году вошли Давид Жеглов, Иван Прохоров и Евгений Яйлоян из Москвы и Михаил Хандохин из Нижнего Новгорода. Руководитель сборной – профессор Московского государственного университета имени М.В. Ломоносова Александр Рубцов, заместители – доцент МГУ Галина Белякова, старший преподаватель МГУ Евгений Шилов, аспирант МГУ Виктория Лавренова. Результаты опубликуют 23 июля.

«Эффективность принятой в «Сириусе» системы выявления и поддержки талантов лучше всего доказывают успехи, которые наши сборные из года в год делают на международных олимпиадах, – сказал заместитель руководителя Образовательного центра «Сириус» Алексей Горбачев. – Мы создаем среду, в которой одаренные дети из всех регионов России учатся у ярких и профессиональных педагогов, работают в компании ребят того же уровня, что и они сами. Всероссийская олимпиада школьников, дистанционные этапы которой с этого года также координирует «Сириус», дает возможность заинтересовать олимпиадным движением как можно больше учащихся в регионах, давая им возможность найти приложение своим способностям и мотивируя учиться лучше. Желаем удачи нашим командам на международных соревнованиях и ждем новых побед».

 

российских школьников завоевали шесть медалей на Международной математической олимпиаде в Санкт-Петербурге

Математика определяет развитие общества, а интеллектуальные соревнования помогают учащимся развивать свои таланты и добиваться успеха. Об этом заявил министр образования Сергей Кравцов на торжественной он-лайн церемонии закрытия 61-й Международной математической олимпиады школьников. Сборная России завоевала на соревнованиях две золотые и четыре серебряные медали, а в неофициальном общекомандном зачете заняла второе место после Китая.

Пресс-служба Министерства образования Российской Федерации

В этом году Санкт-Петербург впервые принимал Международную математическую олимпиаду. Конкурс проходил в дистанционном формате и собрал более 600 юных математиков из 108 стран мира. Конкурс проходил в Российском государственном педагогическом университете имени Герцена.

На торжественной он-лайн церемонии закрытия олимпиады всех ее участников поздравил министр образования Сергей Кравцов.

«61-я Международная математическая олимпиада подарила нам общение с талантливыми и увлеченными учениками из разных стран мира, способными упорно трудиться для достижения блестящих результатов в жизни и будущей профессии, — сказал Сергей Кравцов.

Министр подчеркнул, что интеллектуальные конкурсы помогают талантливым детям еще в школе «раскрыть новые грани своей личности, обрести уверенность в себе и получить дополнительный стимул для дальнейшего развития.»

Глава Минобразования особо поблагодарил всех педагогов, которые вооружили качественными знаниями и помогли детям добиться успехов.

«Учитель не только преподает предмет, но и обучает и помогает учащимся в решении тех или иных задач. Многие ученики ориентируются на своего учителя, от учителя зависит качество образования и успешность каждого ученика», — сказал Сергей Кравцов.

Министр также поблагодарил всех, кто «обеспечил проведение Конкурса на высоком профессиональном уровне и сумел создать для детей настоящую праздничную атмосферу.»

Обладатели медалей:

Данила Демин (гимназия № 8, Сочи, Краснодарский край) — золото;

Алексей Львов (образовательный центр — Гимназия № 6 «Горностай», г. Новосибирск) — золото;

Иван Гайдай-Турлов (СОШ № 57, г.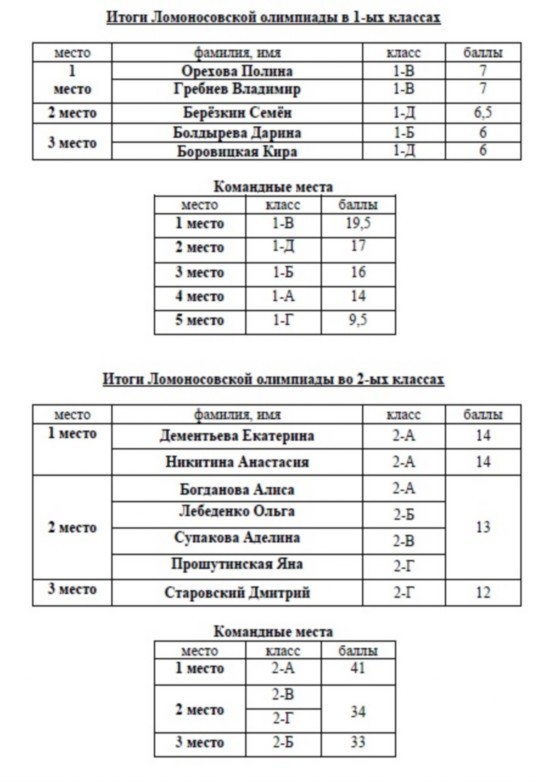 Москва) – серебро;

Антон Садовничий (Вторая школа-лицей, г. Москва) — серебро;

Данил Сибгатуллин (специализированный учебно-научный центр (факультет) – школа-интернат им. А.Н. Колмогорова, МГУ им. М.В. Ломоносова) – серебро;

Максим Туревский (Президентский физико-математический лицей №1 г.239, Санкт-Петербург) — серебро.

Н. Н. Константинов, А. Л. Семенов, «Продуктивное обучение в математической школе», Чебышевский сб., 22:1 (2021), 413–446

ИСТОРИЯ МАТЕМАТИКИ И ПРИМЕНЕНИЯ Продуктивное обучение в математической школе Н. Н. Константинов а , А.Л. Семенова бк а Школа 179 Департамента образования и науки города Москвы (Москва) б Московский государственный университет имени М. В. Ломоносова (Москва) c Институт Акселя Берга Кибернетика и образовательная информатика ФИЦ СКС РАН (Москва) Резюме: В статье рассматриваются причины, по которым математические школы (матшколы) стали важным и весьма продуктивным явлением в российском образовании в последние десятилетия.Краткая характеристика современной модели продуктивного образования восходит к сложившейся традиции обучения в математических школах, что может привести к построению воспроизводимой модели продуктивного образования не только для профильного обучения математике, но и для других направлений российской общеобразовательной школы. образование. Ключевые слова: традиции математических школ и математических классов, Константиновская школа, школьное математическое образование в России, продуктивное обучение, решение неожиданных задач, рекреационная математика, математический кружок, математическая олимпиада, студенты вуза как учителя, уровневая дифференциация, учебно-исследовательская деятельность студентов, цифровая преобразование образования. DOI: https://doi.org/10.22405/2226-8383-2018-22-1-413-446 Полный текст: PDF-файл (593 КБ) УДК: 517 Поступило: 14.12.2020 Принято: 21.02.2021 Ссылка: Н. Н. Константинов, А. Л. Семенов, “Продуктивное обучение в математической школе”, Чебышевский сб., 22:1 (2021), 413–446 Цитирование в формате AMSBIB \RBibitem{KonSem21} \by Н.~Н.~Константинов, А.~Л.~Семенов \paper Продуктивное обучение в математической школе \jour Чебышевский сб. \год 2021 \том 22 \выпуск 1 \страниц 413--446 \mathnet{http://mi.mathnet.ru/cheb1011} \crossref{https://doi.org/10.22405/2226 -8383-2018-22-1-413-446} Варианты подключения: http://mi.mathnet.ru/rus/cheb1011 http://mi.mathnet.ru/rus/cheb/v22/i1/p413 Ссылки на статьи в Google Scholar: русские цитаты, английские цитаты Похожие статьи в Google Scholar: русские статьи, английские статьи

7 7 Количество просмотров: Эта страница: 26 Полный текст: 24 москвичей в составе сборной России заняли второе место на Международной математической олимпиаде | КХАН36 Подведены итоги 61-й Международной математической олимпиады. За награду боролись более 600 студентов из 105 стран мира. Сборная России, в состав которой вошли три московских студента, заняла второе место в неофициальном общекомандном зачете. Серебряные медали завоевали Антон Садовничий из лицея «Вторая школа», Иван Гайдай-Турлов из школы № 57 и Даниил Сибгатуллин из Специализированного учебно-научного центра — школы-интерната имени А. Н. Колмогорова при МГУ. В состав команды также вошли ребята из Санкт-Петербурга, Краснодарского края и Новосибирской области.На счету российских школьников две золотые и четыре серебряные медали. Команду возглавили учитель математики Президентского физико-математического лицея № 239 (Санкт-Петербург) Кирилл Сухов и преподаватели Московского центра повышения квалификации Владимир Брагин и Андрей Кушнир. Международная математическая олимпиада проводилась в дистанционном формате и включала два тура. Они состоялись 21 и 22 сентября. Задача участников составила 4,5 часа. Также для команд прошли онлайн-лекции, экскурсии, дистанционные развлечения. Имена победителей были объявлены 28 сентября на виртуальной церемонии закрытия. Участники получат свои награды по почте. Подробная информация и результаты конкурса опубликованы на официальном сайте. Научный руководитель Центра педагогического мастерства Иван Ященко считает, что полученные результаты свидетельствуют о высоком уровне математического образования в Москве. успеха на олимпиадах международного уровня вдохновляют ребят на новые победы.Сейчас стартует школьный этап Всероссийской олимпиады, также можно поучаствовать в турнире имени М. В. Ломоносова, записаться в математические классы и кружки. За год москвичи завоевали 14 золотых медалей на международной олимпиаде из Москвы завоевали золото на международной математической олимпиаде в Румынии Международная математическая олимпиада проводится с 1959 года. Соревнования проводятся в два тура по три задачи в каждом. Задания охватывают разные области школьной математики, чаще всего геометрию, теорию чисел, алгебру и комбинаторику. Организатором Олимпиады в этом году выступил Санкт-Петербург. В этом же городе пройдет Олимпиада в следующем году. В Москве большое внимание уделяется преподаванию математики. На базе профильных клубов и школ действует образовательный проект «Математическая иерархия». Он направлен на предпрофильную подготовку по математике и смежным специальностям. студентов Университета ИТМО обсудили будущее образования с Владимиром Путиным Сегодня, 25 января, Президент Владимир Путин провел встречу со студентами ведущих вузов России из четырех городов — Москвы, Санкт-Петербурга, Санкт-Петербурга.Петербурга, Новосибирска и Нижнего Новгорода. Среди них четыре студента Университета ИТМО, победители олимпиад по математике и программированию. Они обсудили с президентом важность новых образовательных моделей и условий. Приняли участие студенты математических и информационных специальностей, победители российских и международных олимпиад, таких как Международная математическая олимпиада (ИМО) и Международная олимпиада по математике (ИМС), а также Международная студенческая олимпиада по программированию (ICPC) на совещании, которое проходило в режиме видеосвязи. Среди участников были студенты МГУ им. Ломоносова, МФТИ, СПбГУ, Новосибирского государственного университета, Нижегородского государственного университета им. Лобачевского, Университета ИТМО, который представляли четыре студента факультета информационных технологий и факультет программирования. Михаил Галибов два года назад выиграл Курчатовскую олимпиаду по математике; Александр Елисеев побеждал в различных математических олимпиадах для школьников три года подряд – с 2019 по 2021 год; Виталий Егоров стал золотым призером прошлогодней олимпиады школьников по информатике и программированию; а Даниил Казанцев стал победителем Google Science Fair за разработку системы реабилитации людей с нарушениями слуха и речи (подробнее об этом читайте здесь). К разговору также присоединились Министр науки и высшего образования России Валерий Фальков и помощник президента РФ Андрей Фурсенко . Как отметил президент, Россия всегда славилась своими математиками – именно благодаря фундаменту, заложенному Александром Александровым, Андреем Колмогоровым и другими выдающимися учеными, российские школьники и студенты до сих пор доминируют на различных международных олимпиадах.В то же время математика никогда не была абстрактной областью знаний — эта наука лежит в основе ключевых технологий, поэтому крайне важно обеспечить качественное образование в этой области. Студенты поделились с президентом своими идеями, как проводить такое обучение. Они обсудили, как должны развиваться физико-математические школы, в том числе за пределами крупных городов, какая поддержка нужна молодым ученым и как сделать математическое образование более привлекательным для школьников.Студенты Университета ИТМО акцентировали внимание на разработке новых моделей образования, комфортной среды в вузах, а также рассказали о строительстве ИТМО Хайпарк — научно-образовательного и инновационного центра мирового уровня, который разместится в городе-спутнике Южном. По мнению Михаила Галибова, мы должны перейти на новые модели обучения, если хотим создать эффективную образовательную систему. Провести четыре года в бакалавриате и два года в магистратуре уже не получится.Михаил предлагает систему 2+2+2, которая может быть более эффективной и понятной для студентов. В течение двух лет они будут изучать фундаментальные предметы, затем сосредоточатся на факультативных прикладных курсах, чтобы приобрести практические навыки в своей области, а в последние два года они смогут выбрать новую смежную специальность, которая позволит им работать в пересечение разных полей. Михаил учится на первом курсе бакалавриата, но уже знает, чем хочет заниматься в будущем — либо разработкой видеоигр, либо нейротехнологиями и биоинженерией.По его словам, его программа в Университете ИТМО дает возможность выбрать индивидуальную траекторию обучения. Например, студенты могут выбрать курс разработки Android от JetBrains и начать заниматься промышленным программированием во время учебы. «Некоторые из моих одноклассников уже определились с тем, чем они хотят заниматься, и углубленное изучение предметов, которые на самом деле не связаны с их будущей профессией, кажется бессмысленным. Вот почему нам понадобятся следующие два года обучения, чтобы сосредоточиться на конкретных предметах.Думаю, студентам будет гораздо интереснее изучать то, что им действительно нравится и что они хотели бы применить в своей работе. Модули также позволят им изучать смежные области и позволят стать ученым, если они того пожелают. Процесс обучения станет более продуктивным и эффективным. В Университете ИТМО у студентов уже есть возможность принять участие в практических занятиях», — сказал он. В то же время такие образовательные модели невозможны без создания новой среды для обучения и творчества.Одним из ключевых элементов этой среды являются новые локации, где студенты могут учиться и общаться в неформальной обстановке. В Университете ИТМО такие места уже есть — это коворкинги, которые функционируют на двух кампусах и работают круглосуточно. По словам Михаила Галибова, это позволяет формировать более гибкий график, заниматься групповыми проектами и самообразованием. Он добавил, что новые форматы, которые позволяют студентам индивидуализировать свое обучение, также должны стать ключевой концепцией для Хайпарка ИТМО — научно-образовательного и инновационного центра, строящегося в рамках программы «Кампусы мирового класса». В этом отношении его поддержал Владимир Путин. По словам президента, государство уже занимается поддержкой новых форматов образования и они должны лечь в основу учебного процесса в современных университетских городках, сеть которых планируется создать к 2030 году. «Возможность уточнить свою специализацию после двух лет обучения, а затем доработать свое решение в течение последних двух лет, дает нам более гибкую систему обучения. Создание комфортной среды, в том числе коворкингов, также является частью этой концепции. Мы работаем в этой сфере, например, реализуя программу современного кампуса», — сказал он. Владимир Путин также упомянул, что действующая программа «Приоритет-2030», в которой участвуют более 100 ведущих вузов, направлена ​​на комплексную поддержку вузов. «Мы должны сосредоточиться на создании комфортной образовательной среды.Мы продолжим работать над этим, но мы также надеемся получить отзывы от студентов, чтобы узнать, что работает, а что следует изменить», — сказал он. Среди прочих тем участники обсудили размер студенческих стипендий и грантов для победителей конкурса. По словам Владимира Путина, талантливые российские школьники и студенты регулярно приносят своей стране победы на международных олимпиадах по математике и информатике и заслуживают поощрения. Помощник президента Андрей Фурсенко отметил, что за таких студентов конкурируют крупные компании, а министр Валерий Фальков добавил, что вузы предоставляют им определенные льготы, например льготы при зачислении. Однако Владимир Путин предложил еще больше улучшить материальное обеспечение победителей конкурса. «Говоря о финансовой поддержке, в том числе о стипендиях, мы предложим возможные варианты. Конечно, эта поддержка должна быть особой», — говорит Валерий Фальков. В 2022 году в России состоится знаковое событие в области математики: 6 июля в Санкт-Петербурге начнется Международный конгресс математиков — крупнейшая и наиболее влиятельная конференция среди ученых в этой области. Как подчеркнул президент, такое масштабное мероприятие Россия принимала лишь однажды, в 1966 году. Ожидается, что конгресс соберет более 5000 ведущих ученых со всего мира. Кроме того, в течение года в ведущих вузах страны будут проходить специальные математические конференции. Авторы/названия по математике «новые» Новые представления Материалы, полученные со среды, 16 февраля 22, по четверг, 17 февраля, 22, объявлено в пятницу, 18 февраля, 22 [ всего 261 запись: 1-261 ] [ показывает до 2000 записей на странице: меньше | подробнее ] Новые материалы для Пт, 18 Фев 22 [1] arXiv:2202. 08263 [pdf, ps, другое] [2] arXiv:2202.08271 [pdf, ps, прочее] [3] arXiv:2202.08277 [pdf, ps, другое] [4] arXiv:2202.08300 [pdf, прочее] [5] arXiv:2202.08302 [pdf, прочее] [6] arXiv:2202.08308 [pdf, ps, другое] [7] arXiv:2202.08315 [pdf, прочее] [8] arXiv:2202.08319 [pdf, ps, другое] [9] arXiv:2202.08321 [pdf, ps, другое] [10] arXiv:2202.08323 [pdf, прочее] [11] arXiv:2202.08327 [pdf, ps, другое] [12] arXiv:2202.08328 [pdf, ps, другое] [13] arXiv:2202.08330 [pdf, ps, другое] [14] arXiv:2202.08334 [pdf, прочее] [15] arXiv:2202.08336 [pdf, ps, другое] [16] arXiv:2202.08339 [pdf, прочее] [17] arXiv:2202. 08343 [pdf, ps, другое] [18] arXiv:2202.08351 [pdf, прочее] [19] arXiv:2202.08352 [pdf, ps, другое] [20] arXiv:2202.08361 [pdf, прочее] [21] arXiv:2202.08363 [pdf, ps, другое] [22] arXiv:2202.08382 [pdf, ps, другое] [23] arXiv:2202.08386 [pdf, ps, другое] [24] arXiv:2202.08387 [pdf, прочее] [25] arXiv:2202.08389 [pdf, ps, другое] [26] arXiv:2202.08390 [pdf, ps, прочее] [27] arXiv:2202.08403 [pdf, ps, другое] [28] arXiv:2202.08404 [pdf, ps, другое] [29] arXiv:2202.08411 [pdf, ps, другое] [30] arXiv:2202.08420 [pdf, прочее] [31] arXiv:2202.08421 [pdf, ps, другое] [32] arXiv:2202.08422 [pdf, ps, другое] [33] arXiv:2202. 08425 [pdf, ps, другое] [34] arXiv:2202.08427 [pdf, ps, прочее] [35] arXiv:2202.08443 [pdf, прочее] [36] arXiv:2202.08447 [pdf, прочее] [37] arXiv:2202.08451 [pdf, ps, другое] [38] arXiv:2202.08457 [pdf, ps, другое] [39] arXiv:2202.08464 [pdf, ps, другое] [40] arXiv:2202.08484 [pdf, ps, другое] [41] arXiv:2202.08486 [pdf, прочее] [42] arXiv:2202.08489 [pdf, ps, прочее] [43] arXiv:2202.08507 [pdf, ps, другое] [44] arXiv:2202.08515 [pdf, прочее] [45] arXiv:2202.08518 [pdf, ps, другое] [46] arXiv:2202.08527 [pdf, прочее] [47] arXiv:2202.08530 [pdf, ps, другое] [48] arXiv:2202.08534 [pdf, прочее] [49] arXiv:2202. 08538 [pdf, прочее] [50] arXiv:2202.08541 [pdf, прочее] [51] arXiv:2202.08545 [pdf, ps, другое] [52] arXiv:2202.08554 [pdf, ps, другое] [53] arXiv:2202.08558 [pdf, прочее] [54] arXiv:2202.08560 [pdf, прочее] [55] arXiv:2202.08565 [pdf, ps, другое] [56] arXiv:2202.08571 [pdf, прочее] [57] arXiv:2202.08573 [pdf, прочее] [58] arXiv:2202.08574 [pdf, ps, прочее] [59] arXiv:2202.08575 [pdf, ps, другое] [60] arXiv:2202.08584 [pdf, прочее] [61] arXiv:2202.08588 [pdf, прочее] [62] arXiv:2202.08592 [pdf, прочее] [63] arXiv:2202.08601 [pdf, прочее] [64] arXiv:2202.08615 [pdf, ps, другое] [65] arXiv:2202. 08617 [pdf, другое] [66] arXiv:2202.08634 [pdf, ps, прочее] [67] arXiv:2202.08636 [pdf, ps, другое] [68] arXiv:2202.08640 [pdf, ps, другое] [69] arXiv:2202.08641 [pdf, ps, другое] [70] arXiv:2202.08642 [pdf, ps, другое] [71] arXiv:2202.08644 [pdf, ps, другое] [72] arXiv:2202.08646 [pdf, ps, другое] [73] arXiv:2202.08652 [pdf, ps, прочее] [74] arXiv:2202.08653 [pdf, ps, другое] [75] arXiv:2202.08664 [pdf, ps, другое] [76] arXiv:2202.08666 [pdf, прочее] [77] arXiv:2202.08677 [pdf, прочее] [78] arXiv:2202.08683 [pdf, ps, другое] [79] arXiv:2202.08684 [pdf, ps, другое] [80] arXiv:2202.08689 [pdf, ps, другое] [81] arXiv:2202. 08693 [pdf, ps, прочее] [82] arXiv:2202.08711 [pdf, ps, прочее] [83] arXiv:2202.08715 [pdf, прочее] [84] arXiv:2202.08718 [pdf, прочее] [85] arXiv:2202.08720 [pdf, прочее] [86] arXiv:2202.08723 [pdf, ps, другое] [87] arXiv:2202.08727 [pdf, ps, другое] [88] arXiv:2202.08731 [pdf, ps, другое] [89] arXiv:2202.08733 [pdf, прочее] [90] arXiv:2202.08738 [pdf, ps, другое] [91] arXiv:2202.08739 [pdf, другое] [92] arXiv:2202.08740 [pdf, прочее] [93] arXiv:2202.08749 [pdf, ps, другое] [94] arXiv:2202.08750 [pdf, ps, другое] [95] arXiv:2202.08753 [pdf, прочее] [96] arXiv:2202.08755 [pdf, ps, другое] [97] arXiv:2202. 08760 [pdf, ps, прочее] [98] arXiv:2202.08763 [pdf, прочее] [99] arXiv:2202.08764 [pdf, прочее] [100] arXiv:2202.08766 [pdf, прочее] [101] arXiv:2202.08767 [pdf, ps, другое] [102] arXiv:2202.08774 [pdf, прочее] [103] arXiv:2202.08775 [pdf, ps, другое] [104] arXiv:2202.08782 [pdf, ps, другое] [105] arXiv:2202.08783 [pdf, ps, прочее] [106] arXiv:2202.08786 [pdf, прочее] [107] arXiv:2202.08787 [pdf, прочее] [108] arXiv:2202.08789 [pdf, прочее] [109] arXiv:2202.08796 [pdf, прочее] [110] arXiv:2202.08797 [pdf, ps, другое] [111] arXiv:2202.08799 [pdf, прочее] [112] arXiv:2202.08800 [pdf, ps, другое] [113] arXiv:2202. 08801 [pdf, прочее] [114] arXiv:2202.08803 [pdf, ps, другое] [115] arXiv:2202.08810 [pdf, ps, другое] [116] arXiv:2202.08811 [pdf, ps, другое] [117] arXiv:2202.08828 [pdf, прочее] [118] arXiv:2202.08829 [pdf, ps, другое] [119] arXiv:2202.08830 [pdf, ps, другое] [120] arXiv:2202.08832 [pdf, ps, прочее] Перекрестные списки на пт, 18 февраля 22 [121] arXiv:2202.07329 (кросс-список из cs.LO) [pdf, другое] [122] arXiv:2202.07530 (кросс-список из cs.LG) [pdf, другое] [123] arXiv:2202.08294 (кросс-список из cond-mat.str-el) [pdf, другое] [124]  arXiv:2202.08297 (перекрестный список из Physics.optics) [pdf, др.] [125] arXiv:2202.08311 (перекрестный список из cs.LG) [pdf, прочее] [126]  arXiv:2202. 08312 (кросс-список из cs.LG) [pdf, другое] [127] arXiv:2202.08377 (кросс-список из quant-ph) [pdf, другое] [128] arXiv:2202.08380 (кросс-список из quant-ph) [pdf, другое] [129] arXiv:2202.08383 (кросс-список из cs.RO) [pdf, другое] [130] arXiv:2202.08400 (кросс-список из cs.RO) [pdf, другое] [131] arXiv:2202.08550 (перекрестный список из cs.LG) [pdf, ps, прочее] [132]  arXiv:2202.08567 (кросс-список из stat.ML) [pdf, ps, другое] [133] arXiv:2202.08596 (кросс-список из cs.CE) [pdf, ps, другое] [134] arXiv:2202.08609 (кросс-список из nlin.CD) [pdf, ps, другое] [135] arXiv:2202.08616 (кросс-список из astro-ph.EP) [pdf, ps, другое] [136]  arXiv:2202.08643 (перекрестный список из Physics.оптика) [pdf, прочее] [137] arXiv:2202. 08645 (кросс-список из nlin.SI) [pdf, ps, другое] [138]  arXiv:2202.08657 (кросс-список из cs.LO) [pdf, ps, другое] [139] arXiv:2202.08663 (кросс-список из hep-th) [pdf, ps, другое] [140] arXiv:2202.08688 (кросс-список из cs.CC) [pdf, ps, другое] [141] arXiv:2202.08707 (кросс-список из nlin.AO) [pdf, другое] [142] arXiv:2202.08728 (перекрестный список из stat.ME) [pdf, прочее] [143] arXiv:2202.08747 (кросс-список из cs.DM) [pdf, другое] [144] arXiv:2202.08788 (кросс-список из cs.LG) [pdf, другое] [145] arXiv:2202.08802 (кросс-список из quant-ph) [pdf, другое] Замены на Пт, 18 Фев 22 [146] arXiv:1003.0006 (заменено) [pdf, ps, другое] [147] arXiv:1501.00129 (заменен) [pdf, ps, прочее] [148] arXiv:1610. 03837 (заменено) [pdf, ps, другое] [149] arXiv:1806.05140 (заменено) [pdf, другое] [150] arXiv:1807.09909 (заменено) [pdf, ps, другое] [151] arXiv:1809.01556 (заменено) [pdf, ps, другое] [152] arXiv:1812.01384 (заменено) [pdf, ps, другое] [153] arXiv:1903.03309 (заменено) [pdf, другое] [154] arXiv:1907.08115 (заменен) [pdf, прочее] [155] arXiv:1907.12732 (заменено) [pdf, другое] [156] arXiv:1909.08276 (заменено) [pdf, ps, другое] [157] arXiv:1912.02375 (заменено) [pdf, другое] [158] arXiv:1912.03381 (заменено) [pdf, ps, другое] [159] arXiv:2001.05584 (заменено) [pdf, ps, другое] [160] arXiv:2003.05892 (заменено) [pdf, другое] [161] arXiv:2003.08187 (заменен) [pdf, прочее] [162] arXiv:2003. 09082 (заменено) [pdf, ps, другое] [163] arXiv:2004.00523 (заменено) [pdf, другое] [164] arXiv:2006.09133 (заменено) [pdf, ps, другое] [165] arXiv:2006.10340 (заменено) [pdf, ps, другое] [166] arXiv:2007.03959 (заменено) [pdf, ps, другое] [167] arXiv:2008.02889 (заменено) [pdf, ps, другое] [168] arXiv:2008.08437 (заменен) [pdf, ps, прочее] [169] arXiv:2009.12791 (заменено) [pdf, ps, другое] [170] arXiv:2010.11664 (заменено) [pdf, ps, другое] [171] arXiv:2011.07254 (заменено) [pdf, ps, другое] [172] arXiv:2011.07568 (заменено) [pdf, другое] [173] arXiv:2012.06352 (заменено) [pdf, другое] [174] arXiv:2012.10031 (заменено) [pdf, другое] [175] arXiv:2012.11020 (заменен) [pdf, ps, прочее] [176] arXiv:2101. 01721 (заменено) [pdf, другое] [177] arXiv:2101.07860 (заменено) [pdf, другое] [178] arXiv:2101.12288 (заменено) [pdf, другое] [179] arXiv:2102.01198 (заменено) [pdf, ps, другое] [180] arXiv:2102.10408 (заменено) [pdf, другое] [181] arXiv:2103.07885 (заменено) [pdf, ps, другое] [182] arXiv:2103.08970 (заменен) [pdf] [183] ​​arXiv:2103.08981 (заменено) [pdf] [184] arXiv:2103.13963 (заменено) [pdf, другое] [185] arXiv:2103.14183 (заменено) [pdf, ps, другое] [186] arXiv:2104.00168 (заменено) [pdf, ps, другое] [187] arXiv:2104.05907 (заменено) [pdf, ps, другое] [188] arXiv:2104.11954 (заменено) [pdf, ps, другое] [189] arXiv:2104.14368 (заменен) [pdf, др.] [190] arXiv:2105. 02424 (заменено) [pdf, ps, другое] [191] arXiv:2105.04138 (заменено) [pdf, ps, другое] [192] arXiv:2105.06897 (заменено) [pdf, другое] [193] arXiv:2105.09162 (заменено) [pdf, другое] [194] arXiv:2105.11512 (заменено) [pdf, другое] [195] arXiv:2105.14536 (заменено) [pdf, другое] [196] arXiv:2105.14886 (заменен) [pdf, прочее] [197] arXiv:2106.01999 (заменено) [pdf, ps, другое] [198] arXiv:2106.04096 (заменено) [pdf, другое] [199] arXiv:2106.04579 (заменено) [pdf, ps, другое] [200] arXiv:2106.06018 (заменено) [pdf, ps, другое] [201] arXiv:2106.08862 (заменено) [pdf, другое] [202] arXiv:2106.09659 (заменено) [pdf, другое] [203] arXiv:2106.12082 (заменен) [pdf, ps, прочее] [204] arXiv:2106. 15474 (заменено) [pdf, другое] [205] arXiv:2107.00211 (заменено) [pdf, другое] [206] arXiv:2107.00394 (заменено) [pdf, другое] [207] arXiv:2107.01950 (заменено) [pdf, ps, другое] [208] arXiv:2107.02948 (заменено) [pdf, ps, другое] [209] arXiv:2107.03585 (заменено) [pdf, ps, другое] [210] arXiv:2107.05951 (заменен) [pdf, прочее] [211] arXiv:2107.07854 (заменено) [pdf, ps, другое] [212] arXiv:2107.11590 (заменено) [pdf, ps, другое] [213] arXiv:2107.13540 (заменено) [pdf, ps, другое] [214] arXiv:2107.14462 (заменено) [pdf, ps, другое] [215] arXiv:2108.02374 (заменено) [pdf, другое] [216] arXiv:2108.07850 (заменено) [pdf, другое] [217] arXiv:2108.10597 (заменен) [pdf, ps, прочее] [218] arXiv:2108. 12882 (заменено) [pdf, ps, другое] [219] arXiv:2109.07318 (заменено) [pdf, ps, другое] [220] arXiv:2109.10888 (заменено) [pdf, другое] [221] arXiv:2109.10935 (заменено) [pdf, другое] [222] arXiv:2110.01670 (заменено) [pdf, другое] [223] arXiv:2110.01768 (заменено) [pdf, ps, другое] [224] arXiv:2110.07881 (заменен) [pdf, прочее] [225] arXiv:2110.09176 (заменено) [pdf, ps, другое] [226] arXiv:2110.12784 (заменено) [pdf, ps, другое] [227] arXiv:2111.00515 (заменено) [pdf, другое] [228] arXiv:2111.00879 (заменено) [pdf, ps, другое] [229] arXiv:2111.01062 (заменено) [pdf, ps, другое] [230] arXiv:2111.01509 (заменено) [pdf, ps, другое] [231] arXiv:2111.05779 (заменен) [pdf, прочее] [232] arXiv:2111. 09784 (заменено) [pdf, ps, другое] [233] arXiv:2111.11777 (заменено) [pdf, ps, другое] [234] arXiv:2111.11864 (заменено) [pdf, ps, другое] [235] arXiv:2111.14984 (заменено) [pdf, другое] [236] arXiv:2112.01583 (заменено) [pdf, ps, другое] [237] arXiv:2112.04164 (заменено) [pdf, ps, другое] [238] arXiv:2112.06526 (заменен) [pdf, ps, прочее] [239] arXiv:2112.07713 (заменено) [pdf, ps, другое] [240] arXiv:2112.12406 (заменено) [pdf, другое] [241] arXiv:2112.12511 (заменено) [pdf, другое] [242] arXiv:2112.14007 (заменено) [pdf, ps, другое] [243] arXiv:2201.02033 (заменено) [pdf, ps, другое] [244] arXiv:2201.02298 (заменено) [pdf, другое] [245] arXiv:2201.03759 (заменен) [pdf, прочее] [246] arXiv:2201. 04094 (заменено) [pdf, ps, другое] [247] arXiv:2201.07329 (заменено) [pdf, ps, другое] [248] arXiv:2201.11100 (заменено) [pdf, ps, другое] [249] arXiv:2201.12878 (заменено) [pdf, ps, другое] [250] arXiv:2201.12968 (заменено) [pdf, ps, другое] [251] arXiv:2202.00060 (заменено) [pdf, другое] [252] arXiv:2202.01477 (заменен) [pdf, ps, прочее] [253] arXiv:2202.01591 (заменено) [pdf, ps, другое] [254] arXiv:2202.02637 (заменено) [pdf, ps, другое] [255] arXiv:2202.02726 (заменено) [pdf, другое] [256] arXiv:2202.04052 (заменено) [pdf, другое] [257] arXiv:2202.07032 (заменено) [pdf, ps, другое] [258] arXiv:2202.07236 (заменено) [источник] [259] arXiv:2202.07601 (заменен) [pdf, прочее] [260] arXiv:2202. 07908 (заменено) [pdf, другое] [261] arXiv:2202.08014 (заменено) [pdf, другое] [ всего 261 запись: 1-261 ] [ показывает до 2000 записей на странице: меньше | подробнее ] Отключить MathJax (что такое MathJax?) Ссылки на: arXiv, интерфейс формы, найти, математика, последние, 2202, контакт, помощь (Информация о ключе доступа) туркменских школьников завоевали 22 медали на Международной математической олимпиаде 22 медали разного достоинства – это блестящий итог участия студентов из Туркменистана в 15-й Международной интернет-олимпиаде по математике, проводимой под эгидой Ариэльского университета Государства Израиль. Решением жюри олимпиады команда Туркменского государственного архитектурно-строительного института под руководством капитана, студента университета Джепбара Аскерова награждена золотой медалью. 11 серебряных и 10 бронзовых медалей по праву получили сборные команды Туркменского государственного университета имени Махтумкули, Государственного энергетического института Туркменистана (г. Мары), Туркменского сельскохозяйственного института (г. Дашогуз), Института международных отношений Министерства иностранных дел страны, Международного университета гуманитарных наук и развития, Туркменского государственного педагогического института им. Сейди (г. Туркменабад), Инженерно-технического института, транспортных коммуникаций Туркменистана и Инженерно-технологического университета Туркменистан. Соревнование состояло из двух частей: командного блица и командного первенства. Оно проводилось на трех языках: английском, русском и иврите. В математической олимпиаде приняли участие более 400 школьников в составе 100 команд из 10 стран мира. Среди них США, Великобритания, Беларусь, Польша, Чехия, Россия, Румыния, Индия, Израиль. Туркменистан на олимпиаде представляли студенческие команды из 10 отечественных вузов. Студенты таких крупных зарубежных вузов, как Оксфордский университет (Великобритания), Российский экономический университет им.В. Плеханова, Московский государственный университет имени М.В. Ломоносова (Россия), Ясинский университет имени А.И. Куза (Румыния) и др. Всего по итогам олимпиады названо 86 лучших специалистов по математике из стран-участниц, завоевавших медали различного достоинства. И 22 из них – студенты из Туркменистана, достойно представившие нашу страну на престижном международном шоу. tl2017-math-eng.pdf %PDF-1.4 % 1 0 объект > эндообъект 2 0 объект >поток tl2017-math-eng.pdf Мария Зарубина конечный поток эндообъект 3 0 объект >>> эндообъект 4 0 объект > эндообъект 5 0 объект [0>] эндообъект 6 0 объект >/Родительский 4 0 R/Повернуть на 90/MediaBox[0 0 595 842]/TrimBox[0. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт